Giải SBT Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án

25 người thi tuần này 4.6 0.9 K lượt thi 26 câu hỏi

Đề số 1

🔥 Đề thi HOT:

924 người thi tuần này

13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)

12.9 K lượt thi 13 câu hỏi

324 người thi tuần này

16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án

7.7 K lượt thi 16 câu hỏi

142 người thi tuần này

12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)

5.9 K lượt thi 12 câu hỏi

123 người thi tuần này

100 câu trắc nghiệm Mệnh đề - Tập hợp nâng cao (P1)

27 K lượt thi 20 câu hỏi

113 người thi tuần này

10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)

1 K lượt thi 10 câu hỏi

107 người thi tuần này

10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)

2.1 K lượt thi 10 câu hỏi

100 người thi tuần này

100 câu trắc nghiệm Cung và góc lượng giác nâng cao (P1)

16.5 K lượt thi 25 câu hỏi

97 người thi tuần này

10 câu Trắc nghiệm Cung và góc lượng giác có đáp án (Vận dụng)

3.7 K lượt thi 10 câu hỏi

Nội dung liên quan:

Bài tập Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án

lượt thi

1 đề

Bài tập Toán 10 Bài 2. Giải bất phương trình bậc hai một ẩn có đáp án

lượt thi

1 đề

Giải SBT Toán 10 Bài 2. Giải bất phương trình bậc hai một ẩn có đáp án

lượt thi

1 đề

Bài tập Toán 10 Bài 3. Phương trình quy về phương trình bậc hai có đáp án

lượt thi

1 đề

Giải SBT Toán 10 Bài 3. Phương trình quy về phương trình bậc hai có đáp án

lượt thi

1 đề

Bài tập Toán 10 Bài tập cuối chương 7 có đáp án

lượt thi

1 đề

Giải SBT Toán 10 Bài tập cuối chương 7 có đáp án

lượt thi

1 đề

Danh sách câu hỏi:

Câu 1

Tính biệt thức và nghiệm (nếu có) của các tam thức bậc hai sau. Xác định dấu của chúng tại x = -2.

a) $f (x) = - 2 x^{2} + 3 x - 4$

Xem đáp án

Lời giải

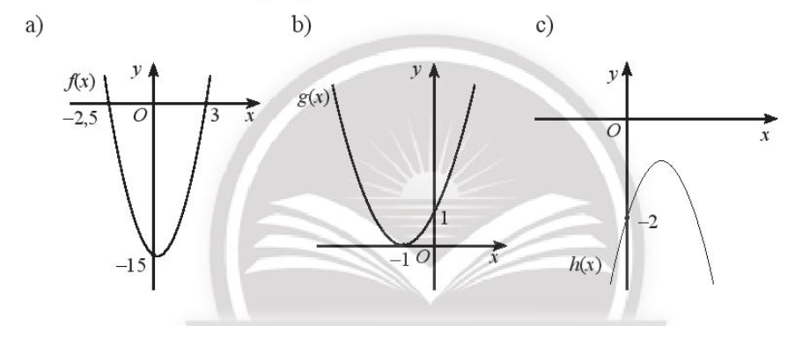
a) Ta có: ∆ = b² – 4ac = 3² – 4.( –2).( –4) = –23 < 0 nên f(x) vô nghiệm và f (x) cùng dấu với a với mọi giá trị x.

Ta lại có: a = 0 – 2 < 0 nên tại x = – 2 thì f(– 2) < 0.

Vì vậy f(x) âm tại x = –2.

Câu 2

b) $g (x) = 2 x^{2} + 8 x + 8;$

Xem đáp án

Lời giải

b) Ta có: ∆ = b² – 4ac = 8² – 4.2.8 = 0 nên g (x) = 0 có nghiệm kép là:

x₀ = $\frac{- b}{2 a} = \frac{- 8}{2.2}$ = – 2. Do đó g (– 2) = 0.

Vì vậy g(x) không âm cũng không dương tại x = –2.

Câu 3

c) $h (x) = 3 x^{2} + 7 x - 10$

Xem đáp án

Lời giải

c) Ta có: ∆ = b² – 4ac = 7² – 4.3.( – 10 ) = 169 > 0 nên h(x) có hai nghiệm phân biệt lần lượt là:

x₁ = $\frac{- b + \sqrt{Δ}}{2a} = \frac{- 7 + \sqrt{169}}{2.3}$ = 1

x₂ = $\frac{- b - \sqrt{Δ}}{2a} = \frac{- 7 - \sqrt{169}}{2.3} = \frac{- 10}{3}$

h(– 2) = 3.(– 2)² + 7.(– 2) – 10 = – 12 < 0.

Vì vậy h(x) âm tại x = – 2.

Câu 4

Tìm các giá trị của tham số m để:

a) $f (x) = (2 m - 8) x^{2} + 2 m x + 1$ là một tam thức bậc hai;

Xem đáp án

Lời giải

a) là tam thức bậc hai khi và chỉ khi 2m – 8 ≠ 0 hay m ≠ 4.

Câu 5

b) $f (x) = (2 m + 3) x^{2} + 3 x - 4 m^{2}$ là một tam thức bậc hai có x = 3 là một nghiệm;

Xem đáp án

Lời giải

b) là tam thức bậc hai khi và chỉ khi 2m + 3 ≠ 0 hay m ≠ $\frac{- 3}{2}$ .

Tam thức có x = 3 là một nghiệm khi và chỉ khi f (3) = (2m + 3) . 3² + 3.3 – 4m² = 0

Suy ra – 4m²+ 18m + 36 = 0 hay – 2m²+ 9m + 18 = 0

Ta có: ∆ = b² – 4ac = 9² – 4.( –2 ).18 = 225 > 0 nên phương trình ẩn m có hai nghiệm phân biệt lần lượt là:

m₁ = $\frac{- b + \sqrt{Δ}}{2a} = \frac{- 9 + \sqrt{225}}{2. (- 2)} = \frac{- 3}{2}$ ( loại vì m ≠ $\frac{- 3}{2}$ )

m₂ = $\frac{- b - \sqrt{Δ}}{2a} = \frac{- 9 - \sqrt{225}}{2. (- 2)}$ = 6.

Vậy m = 6 thỏa mãn f(x) là tam thức bậc hai có x = 3 là một nghiệm.

Câu 6

c) $f (x) = 2 x^{2} + m x - 3$ dương tại x = 2

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Tìm các giá trị của tham số m để:

a) $f (x) = (m^{2} + 9) x^{2} + (m + 6) x + 1$ là một tam thức bậc hai có một nghiệm duy nhất;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

b) $f (x) = (m - 1) x^{2} + 3 x + 1$ là một tam thức bậc hai có hai nghiệm phân biệt;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

c) $f (x) = m x^{2} + (m + 2) x + 1$ là một tam thức bậc hai vô nghiệm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Dựa vào đồ thị của các hàm số bậc hai được cho trong hình dưới đây, xét dấu của tam thức bậc hai tương ứng:

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Xét dấu của các tam thức bậc hai sau:

a) $f (x) = x^{2} - 5 x + 4;$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

b) $f (x) = - \frac{1}{3} x^{2} + 2 x - 3;$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

c) $f (x) = 3 x^{2} + 6 x + 4;$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

d) $f (x) = 3 x^{2} + 6 x + 4;$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

e) $f (x) = - 6 x^{2} + 3 x - 1;$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

g) $f (x) = 4 x^{2} + 12 x + 9$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Tìm các giá trị của tham số m để:

a) $f (x) = (m + 1) x^{2} + 5 x + 2$ là tam thức bậc hai không đổi dấu trên ℝ,

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

b) $f (x) = m x^{2} - 7 x + 4$ là tam thức bậc hai âm với mọi x ∈ ℝ;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

c) $f (x) = 3 x^{2} - 4 x + (3 m - 1)$ là tam thức bậc hai dương với mọi x ∈ ℝ;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

d) $f (x) = (m^{2} + 1) x^{2} - 3 m x + 1$ là tam thức bậc hai âm với mọi x ∈ ℝ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Chứng minh rằng:

a) $2 x^{2} + \sqrt{3} x + 1 > 0$ với mọi x ∈ ℝ;

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

b) $x^{2} + x + \frac{1}{4} \geq 0$ với mọi x ∈ ℝ,

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

c) $- x^{2} < - 2 x + 3$ với mọi x ∈ ℝ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai trong mỗi trường hợp sau:

a) Đồ thị của hàm số đi qua ba điểm có toạ độ là (– 1; – 4), (0; 3) và (1; –14);

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

b) Đồ thị của hàm số y = f(x) đi qua ba điểm có toa độ là (0; –2), (2; 6) và (3; 13);

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

c) f(– 5) = 33, f (0) = 3 và f(2) = l9.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Giải SBT Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án

🔥 Đề thi HOT:

13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)

16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án

12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)

100 câu trắc nghiệm Mệnh đề - Tập hợp nâng cao (P1)

10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)

10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)

100 câu trắc nghiệm Cung và góc lượng giác nâng cao (P1)

10 câu Trắc nghiệm Cung và góc lượng giác có đáp án (Vận dụng)

Nội dung liên quan:

Bài tập Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án

Bài tập Toán 10 Bài 2. Giải bất phương trình bậc hai một ẩn có đáp án

Giải SBT Toán 10 Bài 2. Giải bất phương trình bậc hai một ẩn có đáp án

Bài tập Toán 10 Bài 3. Phương trình quy về phương trình bậc hai có đáp án

Giải SBT Toán 10 Bài 3. Phương trình quy về phương trình bậc hai có đáp án

Bài tập Toán 10 Bài tập cuối chương 7 có đáp án

Giải SBT Toán 10 Bài tập cuối chương 7 có đáp án

Danh sách câu hỏi:

Tính biệt thức và nghiệm (nếu có) của các tam thức bậc hai sau. Xác định dấu của chúng tại x = -2. a) fx=−2x2+3x−4

b) gx=2x2+8x+8;

c) hx=3x2+7x−10

Tìm các giá trị của tham số m để: a) fx=2m−8x2+2mx+1 là một tam thức bậc hai;

b) fx=2m+3x2+3x−4m2 là một tam thức bậc hai có x = 3 là một nghiệm;

c) fx=2x2+mx−3 dương tại x = 2

Tìm các giá trị của tham số m để: a) fx=m2+9x2+m+6x+1 là một tam thức bậc hai có một nghiệm duy nhất;

b) f(x) =( m-1)x2+3x+ 1 là một tam thức bậc hai có hai nghiệm phân biệt;

c) fx=mx2+m+2x+1 là một tam thức bậc hai vô nghiệm.

Dựa vào đồ thị của các hàm số bậc hai được cho trong hình dưới đây, xét dấu của tam thức bậc hai tương ứng:

Xét dấu của các tam thức bậc hai sau: a) fx=x2−5x+4;

b) fx=−13x2+2x−3;

c) fx=3x2+6x+4;

d) fx=3x2+6x+4;

e) fx=−6x2+3x−1;

g) fx=4x2+12x+9

Tìm các giá trị của tham số m để: a) fx=m+1x2+5x+2 là tam thức bậc hai không đổi dấu trên ℝ,

b) fx=mx2−7x+4 là tam thức bậc hai âm với mọi x ∈ ℝ;

c) fx=3x2−4x+3m−1 là tam thức bậc hai dương với mọi x ∈ ℝ;

d) fx=m2+1x2−3mx+1 là tam thức bậc hai âm với mọi x ∈ ℝ.

Chứng minh rằng: a) 2x2+3x+1>0 với mọi x ∈ ℝ;

b) x2+x+14≥0 với mọi x ∈ ℝ,

c) −x2<−2x+3 với mọi x ∈ ℝ.

Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai trong mỗi trường hợp sau: a) Đồ thị của hàm số đi qua ba điểm có toạ độ là (– 1; – 4), (0; 3) và (1; –14);

b) Đồ thị của hàm số y = f(x) đi qua ba điểm có toa độ là (0; –2), (2; 6) và (3; 13);

c) f(– 5) = 33, f (0) = 3 và f(2) = l9.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tính biệt thức và nghiệm (nếu có) của các tam thức bậc hai sau. Xác định dấu của chúng tại x = -2.

a) $f (x) = - 2 x^{2} + 3 x - 4$

b) $g (x) = 2 x^{2} + 8 x + 8;$

c) $h (x) = 3 x^{2} + 7 x - 10$

Tìm các giá trị của tham số m để:

a) $f (x) = (2 m - 8) x^{2} + 2 m x + 1$ là một tam thức bậc hai;

b) $f (x) = (2 m + 3) x^{2} + 3 x - 4 m^{2}$ là một tam thức bậc hai có x = 3 là một nghiệm;

c) $f (x) = 2 x^{2} + m x - 3$ dương tại x = 2

Tìm các giá trị của tham số m để:

a) $f (x) = (m^{2} + 9) x^{2} + (m + 6) x + 1$ là một tam thức bậc hai có một nghiệm duy nhất;

b) $f (x) = (m - 1) x^{2} + 3 x + 1$ là một tam thức bậc hai có hai nghiệm phân biệt;

c) $f (x) = m x^{2} + (m + 2) x + 1$ là một tam thức bậc hai vô nghiệm.

Xét dấu của các tam thức bậc hai sau:

a) $f (x) = x^{2} - 5 x + 4;$

b) $f (x) = - \frac{1}{3} x^{2} + 2 x - 3;$

c) $f (x) = 3 x^{2} + 6 x + 4;$

d) $f (x) = 3 x^{2} + 6 x + 4;$

e) $f (x) = - 6 x^{2} + 3 x - 1;$

g) $f (x) = 4 x^{2} + 12 x + 9$

Tìm các giá trị của tham số m để:

a) $f (x) = (m + 1) x^{2} + 5 x + 2$ là tam thức bậc hai không đổi dấu trên ℝ,

b) $f (x) = m x^{2} - 7 x + 4$ là tam thức bậc hai âm với mọi x ∈ ℝ;

c) $f (x) = 3 x^{2} - 4 x + (3 m - 1)$ là tam thức bậc hai dương với mọi x ∈ ℝ;

d) $f (x) = (m^{2} + 1) x^{2} - 3 m x + 1$ là tam thức bậc hai âm với mọi x ∈ ℝ.

Chứng minh rằng:

a) $2 x^{2} + \sqrt{3} x + 1 > 0$ với mọi x ∈ ℝ;

b) $x^{2} + x + \frac{1}{4} \geq 0$ với mọi x ∈ ℝ,

c) $- x^{2} < - 2 x + 3$ với mọi x ∈ ℝ.

Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai trong mỗi trường hợp sau:

a) Đồ thị của hàm số đi qua ba điểm có toạ độ là (– 1; – 4), (0; 3) và (1; –14);