Giải VTH Toán 8 KNTT Bài 34. Ba trường hợp đồng dạng của hai tam giác có đáp án
47 người thi tuần này 4.6 503 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 10 (có đáp án)
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 8 (có đáp án)
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 1
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
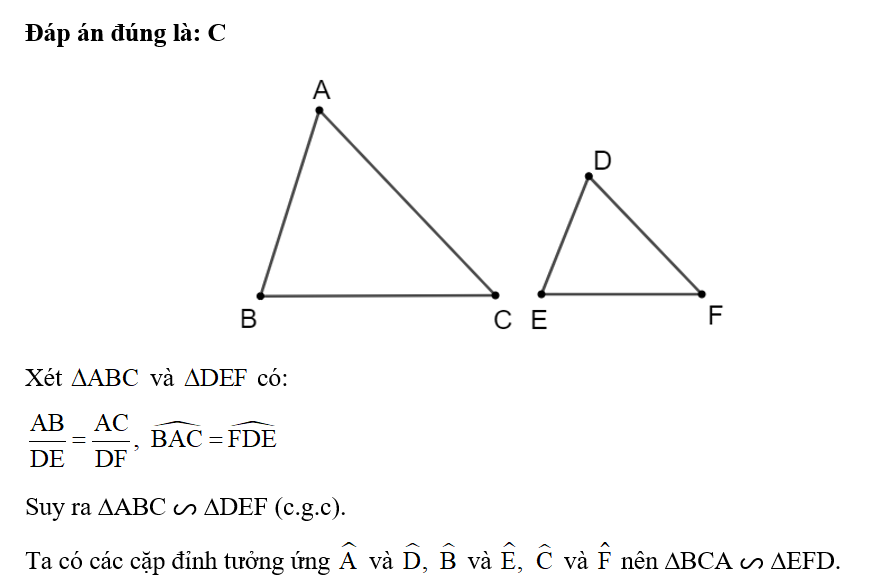
Đáp án đúng là: C
Ta có: nên bộ ba độ dài trong đáp án C là độ dài ba cạnh của tam giác thỏa mãn yêu cầu.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
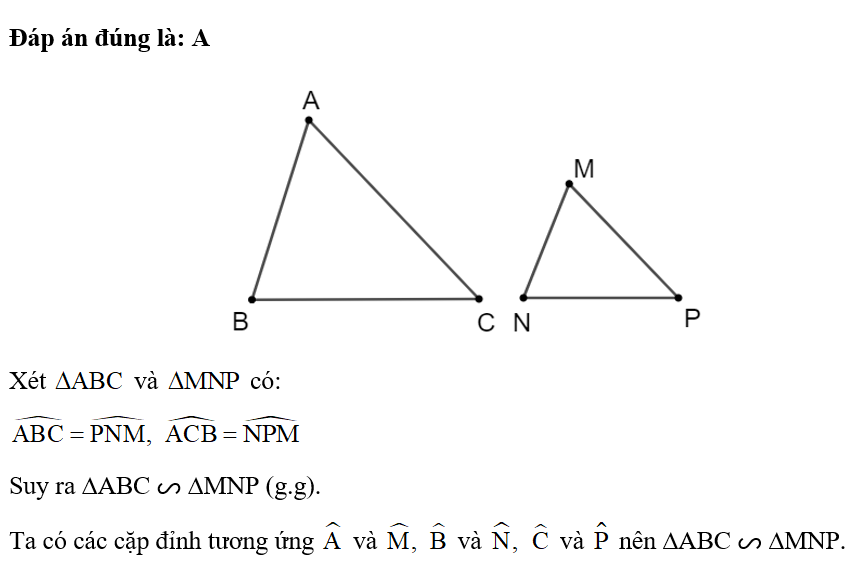
Lời giải
Các giả thiết a hoặc c sẽ suy ra hai tam giác đồng dạng theo các trường hợp (c.c.c) hoặc (g.g). Các giả thiết b hoặc d không suy ra hai tam giác đồng dạng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Vì a + b + c = 33 (cm) và nên bộ ba trong câu a là độ dài ba cạnh của tam giác thỏa mãn yêu cầu. Các bộ ba còn lại hoặc không có tổng bằng 33 (cm) hoặc không có tỉ lệ bằng (4 : 8 : 10) nên không thể là độ dài ba cạnh của tam giác thỏa mãn yêu cầu.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 1/7 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập