Giải SGK Toán 8 KNTT Bài Luyện tập chung trang 55 có đáp án
30 người thi tuần này 4.6 710 lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 9
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Danh sách câu hỏi:
Lời giải
a) Đồ thị hàm số y = 2x – 1 là một đường thẳng đi qua hai điểm là (0; –1) và .
Đồ thị hàm số y = –x + 2 là một đường thẳng đi qua hai điểm là (0; 2) và (2; 0).
Đồ thị của hai hàm số đã cho như hình sau:
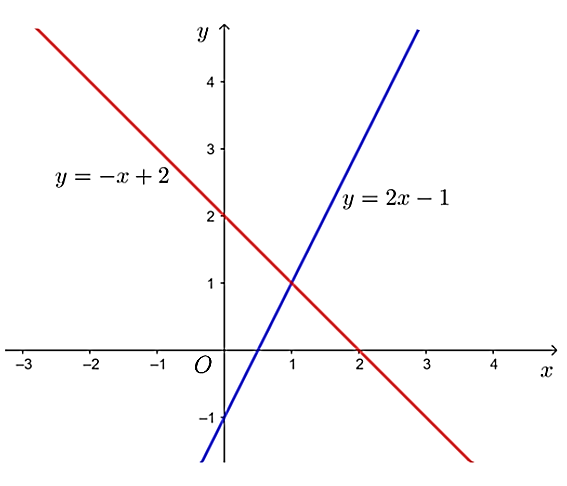
b) Phương trình hoành độ giao điểm của đồ thị hai hàm số là
2x – 1 = –x + 2
3x = 3
x = 1
Thay x = 1 vào hàm số y = 2x – 1, ta được y = 2 . 1 – 1 = 1.
Vậy tọa đô giao điểm của hai đồ thị hàm số trên là điểm A (1; 1).
Lời giải
Hàm số y = (3 – m)x + 2m + 1 là hàm số bậc nhất khi 3 – m ≠ 0, hay m ≠ 3.
a) Vì đồ thị đi qua điểm (1; 2) nên ta có:
2 = (3 – m).1 + 2m + 1
2 = 3 – m + 2m + 1
m = –2.
Giá trị này của m thỏa mãn điều kiện m ≠ 3.
Vậy giá trị m cần tìm là m = –2.
b) Vì đường thẳng y = x + 1 cắt trục tung tại điểm (0; 1) nên để đường thẳng đã cho cắt đường thẳng y = x + 1 tại một điểm nằm trên trục tung thì đường thẳng y = (3 – m)x + 2m + 1 phải đi qua điểm (0; 1). Từ đó suy ra
1 = (3 – m) . 0 + 2m + 1 hay m = 0.
So sánh với điều kiện ta thấy m = 0 thỏa mãn.
Vậy giá trị m cần tìm là m = 0.
Lời giải
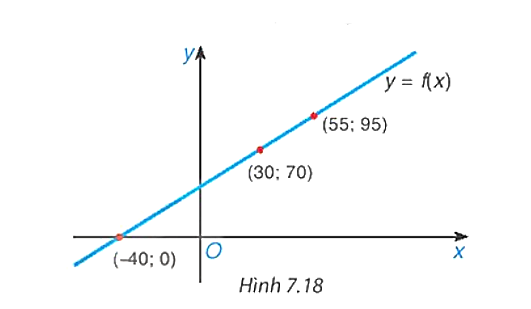
Từ đồ thị đã cho, ta thấy:
a) f(x) = 70 khi x = 30;
b) f(x) = 95 khi x = 55;
c) f(x) = 0 khi x = – 40.
Lời giải
Điều kiện: 1 < x ≤ 30.
a) Thay x = 20 vào công thức đã cho, ta có:
T(20) = 10 000 + 13 600 . (20 – 1) = 268 400 (đồng).
Vậy số tiền phải trả khi xe di chuyển 20 km là 268 400 đồng.
b) Nếu một hành khách phải trả 200 400 đồng, tức là T(x) = 200 400. Từ đây, ta có phương trình: 200 400 = 10 000 + 13 600.(x – 1)
13 600.(x – 1) = 190 400
x – 1 = 190 400 : 13 600
x – 1 = 14
x = 15 (thỏa mãn điều kiện).
Vậy hành khách đó đã di chuyển 15 km.
Lời giải
a) Vì mỗi năm giá trị của chiếc máy photocopy sẽ giảm 6 triệu đồng nên x năm thì giá trị của chiếc máy này sẽ giảm 6x triệu đồng.
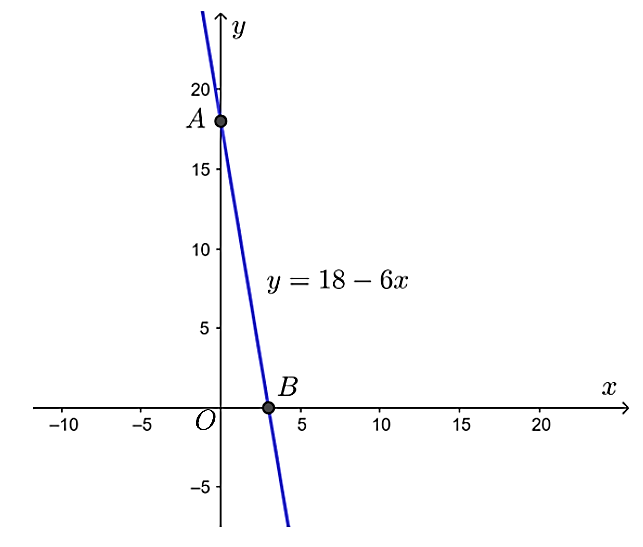
Do đó, hàm số bậc nhất biểu thị giá trị sổ sách của máy photocopy là V(x) = 18 – 6x.
b) Vẽ đồ thị hàm số y = V(x) = 18 – 6x.
Cho x = 0 thì y = 18, ta được giao điểm của đồ thị với trục Oy là A(0; 18).
Cho y = 0 thì x = 3, ta được giao điểm của đồ thị với trục Oy là B(3; 0).
Đồ thị hàm số y = 18 – 6x là đường thẳng AB.
c) Giá trị sổ sách của máy sau 2 năm sử dụng, tức với x = 2 là:
V(2) = 18 – 6 . 2 = 18 – 12 = 6 (triệu đồng).
d) Để có giá trị sổ sách là 9 triệu đồng thì V(x) = 9, tức là 9 = 18 – 6x, suy ra x = 1,5.
Vậy sau 1,5 năm sử dụng thì máy photocopy có giá trị sổ sách là 9 triệu đồng.