20 câu trắc nghiệm Toán 10 Kết nối tri thức Bài 4. Hệ bất phương trình bậc nhất hai ẩn (Đúng sai - trả lời ngắn) có đáp án
56 người thi tuần này 4.6 324 lượt thi 20 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Đáp án đúng là: C
Nhận xét: chỉ có điểm \[\left( {0;0} \right)\] không thỏa mãn hệ.
Câu 2
Lời giải
Đáp án đúng là: C
Nhận xét: chỉ có điểm \[\left( {0; - 2} \right)\] thỏa mãn hệ.
Câu 3
Lời giải
Đáp án đúng là: C
Thế đáp án, chỉ có \(x = 1;y = - \frac{1}{2}\) thỏa mãn hệ bất phương trình \( \Rightarrow \) chọn C.
Câu 4
Lời giải
Đáp án đúng là: D
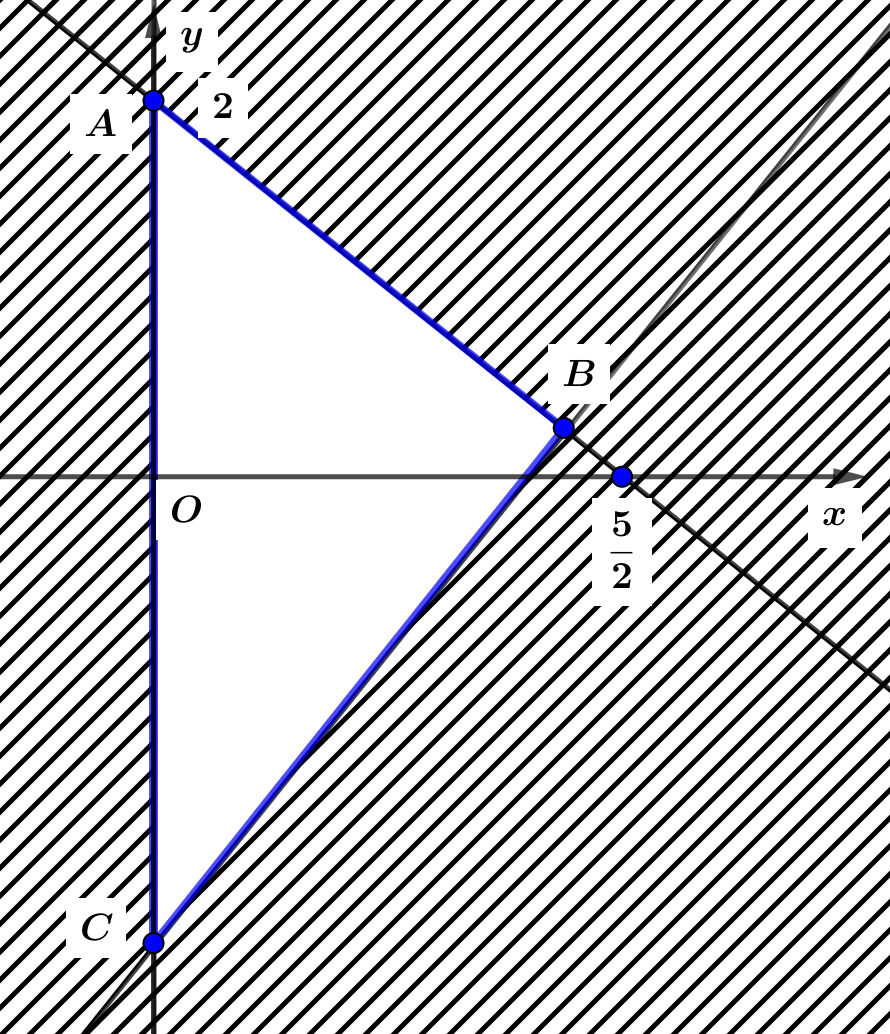
Cạnh \[AC\] có phương trình \[x = 0\] và cạnh \[AC\] nằm trong miền nghiệm nên \[x \ge 0\] là một bất phương trình của hệ.
Cạnh \[AB\] qua hai điểm \[\left( {\frac{5}{2};\;0} \right)\] và \[\left( {0;\;2} \right)\] nên có phương trình \[\frac{x}{{\frac{5}{2}}} + \frac{y}{2} = 1 \Leftrightarrow 4x + 5y = 10\].
Vậy hệ bất phương trình cần tìm là \(\left\{ \begin{array}{l}x \ge 0\\5x - 4y \le 10\\4x + 5y \le 10\end{array} \right.\).
Câu 5
Lời giải
Đáp án đúng là: A
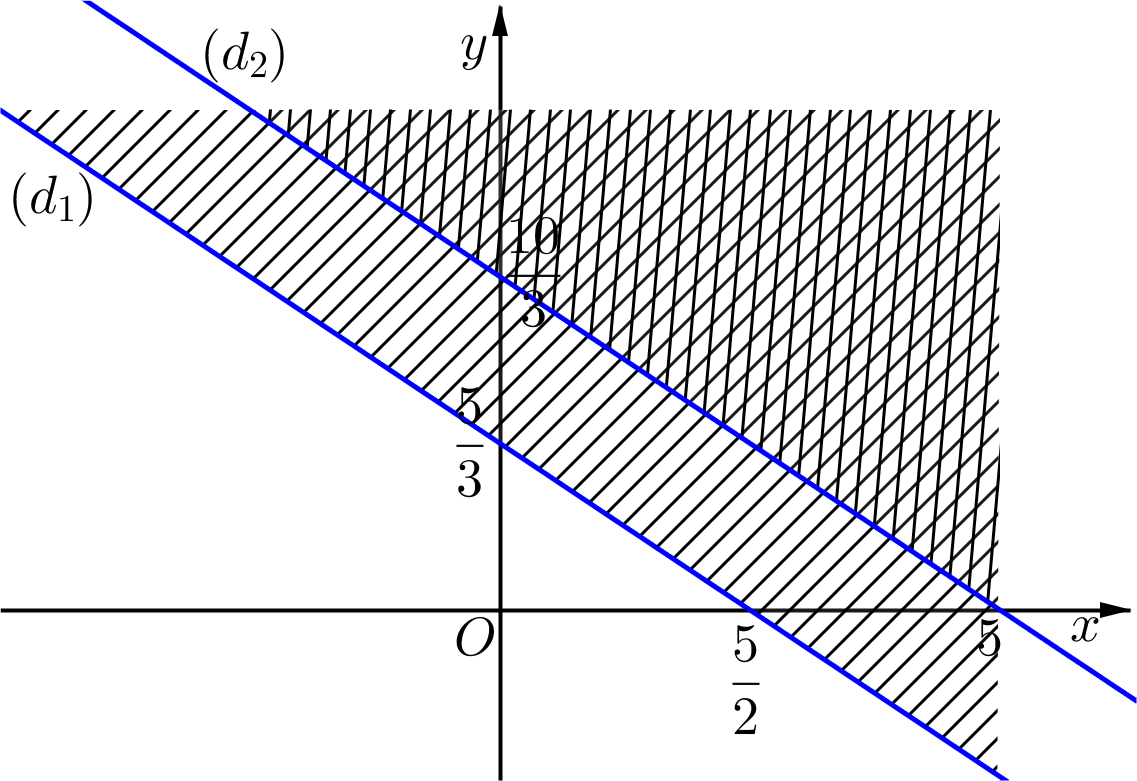
Trước hết, ta vẽ hai đường thẳng:
\(\left( {{d_1}} \right):2x + 3y = 5\)
\(\left( {{d_2}} \right):x + \frac{3}{2}y = 5\)
Ta thấy \(\left( {0\,\,;\,\,0} \right)\) là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Say khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ.
Từ đó, ta suy ra \({S_1} = S\) và \({S_1} \subset {S_2}\).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.