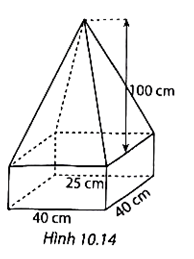
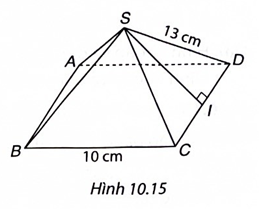
Giải vở thực hành Toán 8 KNTT Bài 39. Hình chóp tứ giác đều
21 người thi tuần này 4.6 338 lượt thi 11 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
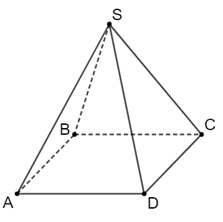
Lời giải
Đáp án đúng là: C
Diện tích xung quanh của hình chóp tứ giác đều bằng tích của nửa chu vi đáy với trung đoạn.
Lời giải
Đáp án đúng là: B
Thể tích của hình chóp tứ giác đều có diện tích đáy bằng 100 cm2, chiều cao bằng 9 cm là:
\(V = \frac{1}{3}.100.9 = 300\) (cm3).
Vậy thể tích của hình chóp tứ giác đều là 300 cm3.
Lời giải
Đáp án đúng là: C
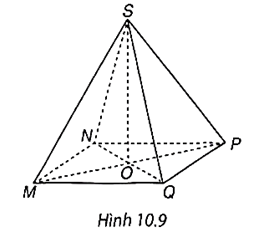
Đường cao trong Hình 10.9 của hình chóp S.MNPQ là SO.
Lời giải
Đáp án đúng là: B
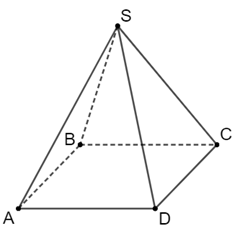
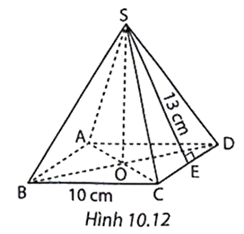
Do diện tích đáy của hình chóp bằng 36 cm2 nên cạnh đáy bằng \(\sqrt {36} = 6\) (cm).
Diện tích xung quanh của hình chóp tứ giác đều này bằng:
\({S_{xq}} = p.d = \frac{{6.4}}{2}.4 = 48\) (cm2).
Vậy diện tích xung quanh của hình chóp tứ giác đều là 48 cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.