20 bài tập Toán 9 Kết nối tri thức Bài 30. Đa giác đều và phép quay có đáp án
53 người thi tuần này 4.6 118 lượt thi 20 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Giữa kì 2 Toán 9 trường THCS Ba Đình (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Mai Dịch (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Chương Dương (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Ban Mai School (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Trần Đăng Ninh (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Mạc Đĩnh Chi (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Phan Chu Trinh (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Ngô Sĩ Liên (Hà Nội) năm học 2024-2025 có đáp án
Danh sách câu hỏi:
Lời giải
Mỗi góc của ngũ giác đều bằng: \(\frac{{(5 - 2){{.180}^0}}}{5}\, = \,{108^0}\)
Mỗi góc của ngũ lục đều bằng: \(\frac{{(6 - 2){{.180}^0}}}{6}\, = \,{120^0}\)
Mỗi góc của bát giác đều bằng: \(\frac{{(8 - 2){{.180}^0}}}{8}\, = \,{135^0}\)
Lời giải
Gọi \[n\] là số cạnh của đa giác đều.
Ta có \[\frac{{\left( {n - 2} \right).180^\circ }}{n} = 135^\circ \]
nên \[\frac{{n - 2}}{n} = \frac{{135}}{{180}} = \frac{3}{4}\].
Do đó \[4\left( {n - 2} \right) = 3n\].
Vậy \[n = 8\].
Lời giải
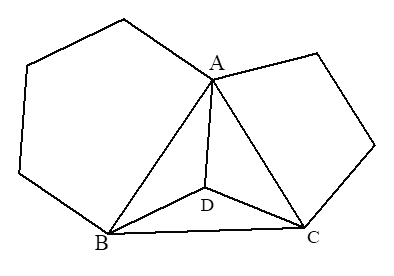
![Bài 3. Cho tam giác đều \[ABC\], các đường cao \[AD\], \[BE\], \[CF\] cắt nhau tại \[H\]. Gọi \[I\], \[K\], \[M\] theo thứ tự là trung điểm của \[HA\], \[HB\], \[HC\]. Chứng minh rằng \[DKFIEM\] là lục giác đều. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/10-1769710972.png)
Xét \[\Delta HDC\] vuông tại \[D\], \[DM\] là đường trung tuyến ứng với cạnh huyền nên \[DM = HM\]. Ta lại có \[\widehat {{C_1}} = 30^\circ \] nên \[\widehat {{H_1}} = 60^\circ \]. Do đó \[\Delta HDM\] là tam giác đều.
Tương tự các tam giác \[HME\], \[HEI\], \[HIF\], \[HFK\], \[HKD\] là các tam giác đều.
Lục giác \[DKFIEM\] có các cạnh bằng nhau và các góc bằng nhau (bằng \[120^\circ \]) nên là lục giác đều.
Lời giải
a) Từ mỗi đỉnh của hình n – giác lồi. kẻ được \[n - 1\] đoạn thẳng đến các đỉnh còn lại, trong đó có hai đoạn thẳng là cạnh của đa giác, \[n - 3\] đoạn thẳng là đường chéo.
Đa giác có \[n\] đỉnh nên kẻ được \[n\left( {n - 3} \right)\] đường chéo, trong đó mỗi đường chéo tính 2 lần. Vậy số đường chéo của hình \[n\]- giác lồi là \[\frac{{n\left( {n - 3} \right)}}{2}\].
b) Giải phương trình \[\frac{{n\left( {n - 3} \right)}}{2} = n\]. Ta được \[n = 5\]
Lời giải
![Bài 5. Cho lục giác đều \[ABCDEF\]. Gọi \[M\] là trung điểm của \[EF\], \[N\] là trung điểm của \[BD\]. Chứng minh rằng \[AMN\] là tam giác đều. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/11-1769711011.png)
Gọi \[O\] là giao điểm của \[AD\], \[BE\], \[CF\]. Dễ dàng chứng minh \[N\] là trung điểm của \[OC\], \[\Delta AFM = \Delta AON\] (c.g.c).
Từ đó \[AM = AN\] và \[\widehat {MAN} = 60^\circ \] nên \[\Delta AMN\] là tam giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hình ngũ giác đều \[ABCDE\]có tâm \(O\) (Hình vẽ). a) Phép quay ngược chiều tâm O biến điểm A thành điểm B thì các điểm \(B,C,D,E\) tương ứng biến thành các điểm nào? b) Chỉ ra ba phép quay tâm O giữ nguyên hình ngũ giác đều đã cho. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/19-1769711285.png)