Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 08
30 người thi tuần này 4.6 620 lượt thi 21 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \[{\log _a}b + {\log _a}c = {\log _a}\left( {b + c} \right)\].
B. \[{\log _a}b + {\log _a}c = {\log _a}\left| {b - c} \right|\].
C. \[{\log _a}b + {\log _a}c = {\log _a}\left( {bc} \right)\].
D. \[{\log _a}b + {\log _a}c = {\log _a}\left( {b - c} \right)\].
Lời giải
Theo tính chất logarit ta có: \[{\log _a}b + {\log _a}c = {\log _a}\left( {bc} \right)\].
Câu 2
A. \(286.408.856\) VNĐ.
B. \(206.075.502\) đồng.
C. \(268.408.856\) đồng.
D. \(260.075.502\) đồng.
Lời giải
Áp dụng công thức tính lãi kép \({T_n} = M{\left( {1 + r} \right)^n}\) với \(n = 72\) tháng (6 năm),\(M = 200.000.000\), \(r = 0.5\% \), ta được \({T_{72}} = 200.000.000{\left( {1 + 0.5\% } \right)^{72}} = 286.408.856\).
Câu 3
Lời giải
Đặt \(t = {3^x}\) \(\left( {t > 0} \right)\), khi đó phương trình trở thành \({t^2} - 3t + 2 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = 2\end{array} \right.\,\,\,\left( {tm} \right)\)
Với \(t = 1\) ta có \({3^x} = 1 \Leftrightarrow x = 0\)
Với \(t = 2\) ta có \({3^x} = 2 \Leftrightarrow x = {\log _3}2\)
Suy ra phương trình có hai nghiệm là \({x_1} = 0\) và \({x_2} = {\log _3}2\)
Vậy \(A = 2{x_1} + 3{x_2}\)\( = 2.0 + 3{\log _3}2\)\( = 3{\log _3}2\).
Câu 4
Lời giải
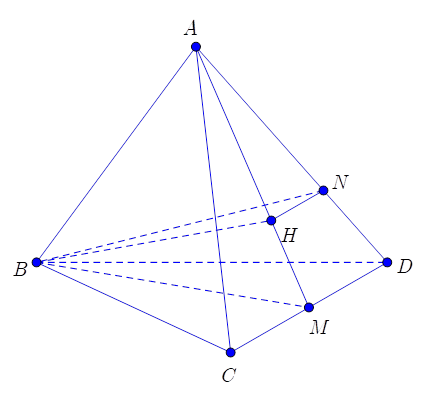
Gọi \(H\) là hình chiếu của \(B\) trên \(\left( {ACD} \right)\). Suy ra \(H\) là tâm tam giác \(ACD\).
Ta có \(\left\{ \begin{array}{l}AM \bot BH\\AM \bot BN\end{array} \right. \Rightarrow AM \bot HN\). Do đó \(HN\;{\rm{//}}\;MD\), suy ra \(\frac{{AN}}{{AD}} = \frac{2}{3}\).
Câu 5
Lời giải
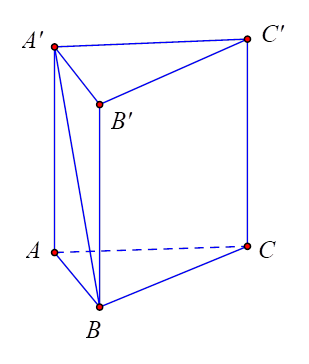
Hình lăng trụ đứng \[ABC.A'B'C'\] nên \[BB' \bot \left( {A'B'C'} \right)\]\[ \Rightarrow BB' \bot A'B'\]\[ \Rightarrow A'B' \bot BB'\] \[\left( 1 \right)\]
Bài ra có \[AB \bot BC\]\[ \Rightarrow A'B' \bot B'C'\].
Kết hợp với \[\left( 1 \right)\] \[ \Rightarrow A'B' \bot \left( {BCC'B'} \right)\] \[ \Rightarrow \widehat {\left( {A'B;\left( {BCC'B'} \right)} \right)} = \widehat {A'BB'}\]
\[ \Rightarrow \tan \widehat {\left( {A'B;\left( {BCC'B'} \right)} \right)} = \tan \widehat {A'BB'}\]\[ = \frac{{A'B'}}{{BB'}}\]\[ = \frac{a}{{a\sqrt 3 }}\]\[ = \frac{1}{{\sqrt 3 }}\]\[ \Rightarrow \widehat {\left( {A'B;\left( {BCC'B'} \right)} \right)} = 30^\circ \].
Câu 6
A. \(\left( {SBD} \right) \bot \left( {ABCD} \right)\).
B. \(\left( {SBC} \right) \bot \left( {ABCD} \right)\).
C. \(\left( {SAD} \right) \bot \left( {ABCD} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(\frac{{{a^3}}}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(\frac{1}{4}\).
B. \(\frac{5}{{12}}\).
C. \(\frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(\frac{3}{{10}}\).
B. \(\frac{1}{2}\).
C. \(\frac{2}{5}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(40\,{\rm{m/}}\,{\rm{s}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
a) Biến cố "Tích hai số ghi trên hai thẻ là một số chẵn" là \(A \cup B\).
b) \(P(A \cup B) = P(A) + P(B)\)
c) \(P(A) < P(B){\rm{ }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
a) \[f'(2) = 2\]
b) \[f(2) = 2\]
c) \(f\left( 2 \right) + f'\left( 2 \right) = 4\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.