Bộ 10 đề thi giữa kì 1 Toán 12 Cánh diều có đáp án - Đề 08
38 người thi tuần này 4.6 7.3 K lượt thi 22 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Đáp án đúng là: B
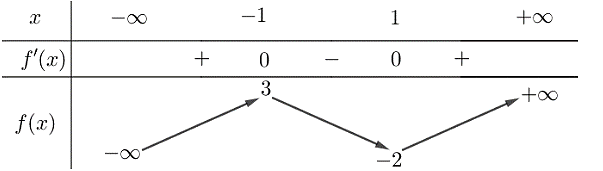
Từ bảng biến thiên, ta thấy hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).
Lời giải
Đáp án đúng là: D
Từ bảng biến thiên, ta thấy hàm số đã cho đạt cực tiểu tại \[x = 1\] và giá trị cực tiểu \({y_{CT}} = - 2\).
Câu 3
Lời giải
Đáp án đúng là: A
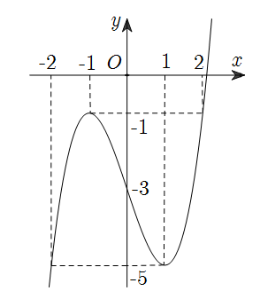
Nhìn vào đồ thị hàm số đã cho, ta thấy:
\(m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 5\) khi \(x = - 2\) hoặc \(x = 1\);
\(M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 1\) khi \(x = - 1\) hoặc \(x = 2\).
Câu 4
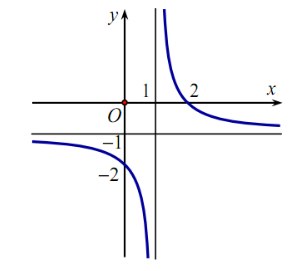
A. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng \(x = 2\) và \(x = - 2\).
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
D. Đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng \(y = 2\) và \(y = - 2\).
Lời giải
Đáp án đúng là: D
Dựa vào định nghĩa đường tiệm cận ngang của đồ thị hàm số, ta có:
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\) và \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 2\) thì đồ thị hàm số đã cho có 2 tiệm cận ngang là các đường thẳng \(y = 2\) và \(y = - 2\).
Câu 5
Lời giải
Đáp án đúng là: D
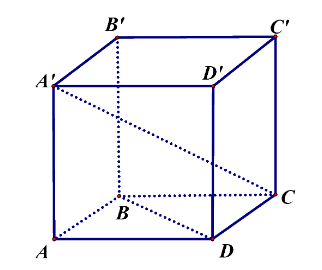
Số vectơ khác vectơ \(\overrightarrow 0 \) mà mỗi vectơ có điểm đầu và điểm cuối là hai đỉnh của tứ diện \(ABCD\) là số các chỉnh hợp chập 2 của 4 phần tử, do đó số vectơ là \(A_4^2 = 12\).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
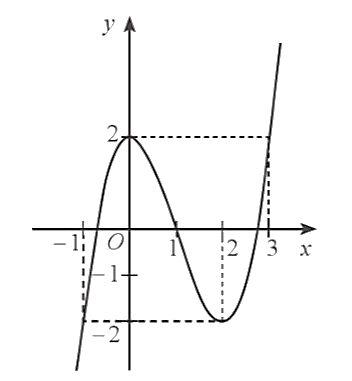
A. Hàm số đã cho đồng biến trên khoảng \(\left( {1; + \infty } \right)\)
B. Hàm số đã cho nghịch biến trên khoảng \(\left( { - 1;3} \right)\).
C. Hàm số đã cho đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\).
D. Hàm số đã cho nghịch biến trên khoảng \(\left( {1;3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.