Đề cương ôn tập giữa kì 1 Toán 12 Kết nối tri thức cấu trúc mới có đáp án - Bài 1. Tính đơn điệu và cực trị của hàm số
72 người thi tuần này 4.6 1.1 K lượt thi 18 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \((0; + \infty )\).
B. \(( - \infty ;0)\).
Lời giải
Hàm số đã cho xác định trên \[{\rm{D}} = \mathbb{R}\].
Có \[y' = - 4{x^3} + 8x\].
Cho \[y' = 0 \Leftrightarrow - 4{x^3} + 8x = 0 \Leftrightarrow 4x( - {x^2} + 2) = 0 \Leftrightarrow \left[ \begin{array}{l}4x = 0\\ - {x^2} + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \end{array} \right.\].
Bảng biến thiên :
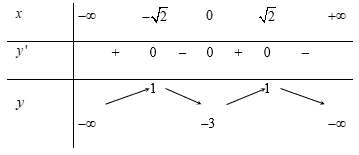
Dựa vào bảng biến thiên, hàm số đồng biến trên: \[\left( { - \infty ; - \sqrt 2 } \right)\] và \[\left( {0;\sqrt 2 } \right)\]. Chọn C.
Câu 2
A. \(( - \infty ;7)\).
B. \(( - \infty ; + \infty )\).
Lời giải
Hàm số đã cho xác định và liên tục trên: \[{\rm{D}} = \mathbb{R}\backslash \left\{ { - 7} \right\}\].
Tính\[y' = \frac{{\left( { - 2} \right).7 - 1.3}}{{{{\left( {x + 7} \right)}^2}}} = \frac{{ - 17}}{{{{\left( {x + 7} \right)}^2}}} < 0,\forall x \in {\rm{D}} = \mathbb{R}\backslash \left\{ { - 7} \right\}\].
Bảng biến thiên:
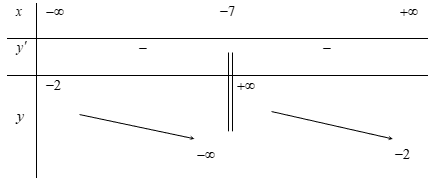
Hàm số đã cho luôn nghịch biến trên: \[\left( { - \infty ; - 7} \right)\] và \[\left( { - 7; + \infty } \right)\]. Chọn C.
Câu 3
A. \(\left( {0;1} \right)\).
Lời giải
Tập xác định \(D = \left[ {0;2} \right]\).
Ta có \(y' = \frac{{1 - x}}{{\sqrt {2x - {x^2}} }}\); \(y' = 0 \Leftrightarrow x = 1\).
Bảng biến thiên:

Vậy hàm số nghịch biến trên khoảng \(\left( {1;2} \right)\). Chọn C.
Câu 4
A. \[y = \frac{{x - 1}}{{x + 2}}\].
B. \[y = {x^3} + 4{x^2} + 3x--1\].
Lời giải
Hàm số \[y = \frac{1}{3}{x^3} - \frac{1}{2}{x^2} + 3x + 1\] có \(y' = {x^2} - x + 3 = {\left( {x - \frac{1}{2}} \right)^2} + \frac{{11}}{4} > 0,\,\forall x \in \mathbb{R}\). Chọn D.
Câu 5
A. (I), (II).
Lời giải
(I): \(y' = - 3{x^2} + 6x - 3 = - 3{\left( {x - 1} \right)^2} \le 0,\forall x \in \mathbb{R}\).
(II):\(y' = \cos x - 2 < 0,\forall x \in \mathbb{R}\).
(III): \(y' = - \frac{{3{x^2}}}{{2\sqrt {{x^3} + 2} }} \le 0,\forall x \in \left( { - \sqrt[3]{2}; + \infty } \right)\).
(IV): \(y' = - \frac{1}{{{{\left( {1 - x} \right)}^2}}} < 0,\forall x \ne 1\). Chọn A.
Câu 6
A. \[x = - 2.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Hàm số đạt cực đại tại \(x = 4.\)
B. Hàm số đạt cực tiểu tại \(x = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(y = 2x + \frac{2}{{x + 1}}.\)
B. \(y = {x^3} + 3{x^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Cho hàm số y = f( x ) liên tục trên đoạn [0;4] có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/blobid1-1757583690.png)