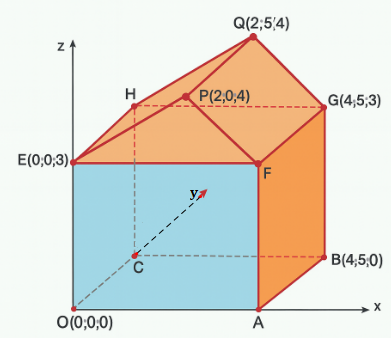
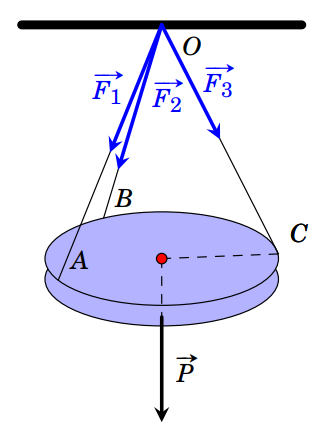
Bộ 20 đề thi Giữa kì 1 Toán 12 Cánh diều có đáp án - Đề 20
20 người thi tuần này 4.6 1.2 K lượt thi 22 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian Oxyz, hình chiếu vuông góc của điểm \(M\left( {4; - 1;3} \right)\)trên mặt phẳng \[\left( {Oyz} \right)\]có tọa độ là:
Lời giải
Chọn C
Hình chiếu của \(M\left( {{x_0};{y_0};{z_0}} \right)\)trên mặt phẳng \[\left( {Oyz} \right)\]có tọa độ là \(\left( {0;{y_0};{z_0}} \right)\).
Câu 2
Lời giải
Chọn D
Ta có
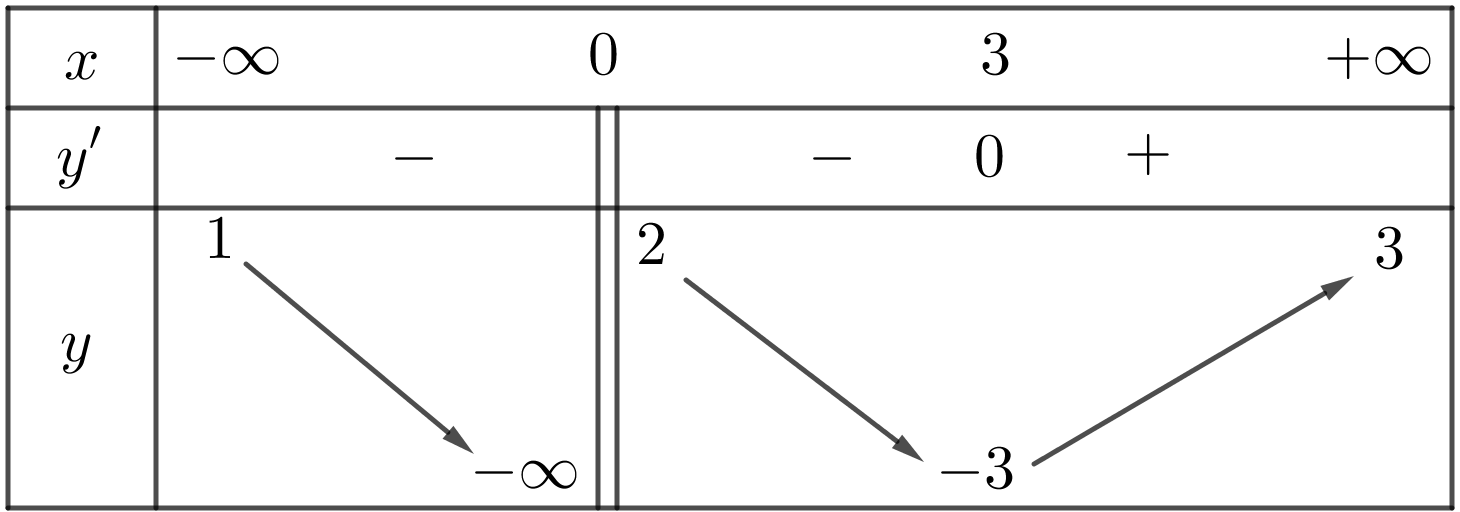
Câu 3
Lời giải
Chọn D
Từ bảng biến thiên ta có: \(\mathop {\lim }\limits_{x \to {0^ - }} y = - \infty \)\( \Rightarrow x = 0\) là đường tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to - \infty } y = 1\) \( \Rightarrow y = 1\) là đường tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to + \infty } y = 3\) \( \Rightarrow y = 3\) là đường tiệm cận ngang.
Vậy đồ thị hàm số có ba đường tiệm cận có phương trình\(x = 0\);\(y = 1\);\(y = 3\).
Câu 4
Lời giải
Chọn A
Phương trình mặt cầu tâm \(I\left( {a,b,c} \right)\) bán kính \(R\) dạng khai triển là :\({x^2} + {y^2} - 2ax - 2by - 2cz + d = 0\), \(d = \sqrt {{a^2} + {b^2} + {c^2} - {R^2}} \)
Theo bài ra ta có:
\(\begin{array}{l}a = \frac{{ - 2}}{{ - 2}} = 1;\,b = \frac{{ - 4}}{{ - 2}} = 2;\,c = \frac{0}{{ - 2}} = 0\\d = 0 \Rightarrow R = \sqrt {{a^2} + {b^2} + {c^2} - d} = \sqrt 5 .\end{array}\)
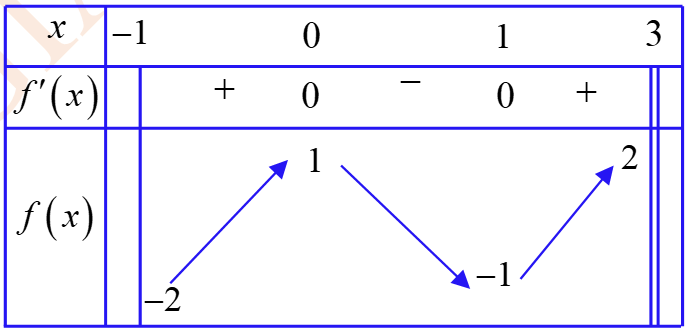
Câu 5
Lời giải
Chọn C
Dựa vào bảng biến thiên ta thấy \(f\left( x \right) \ge - 2\mathop {}\limits_{} \forall x \in \left[ { - 1;3} \right)\) và \(f\left( { - 1} \right) = - 2\) nên \(\mathop {{\rm{min}}}\limits_{x \in \left[ { - 1;3} \right)} f\left( x \right) = - 2\).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.