Bài 10: Đường thẳng song song với một đường thẳng cho trước

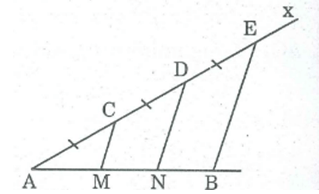
Gọi giao điểm của các đường thẳng kẻ từ C và D song song với BE cắt AB tại M và N.

Ta có: AC = CD = DE (gt)

CM // DN // BE

Theo tính chất đường thẳng song song cách đều, ta có:

AM = MN = NB

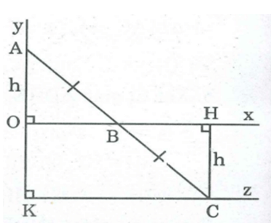
Vì điểm C đối xứng với điểm A qua điểm B nên BA = BC

Kẻ CH ⊥ Ox

Xét hai tam giác vuông AOB và CHB, ta có:

$\angle$(AOB) = $\angle$(CHB ) = ${90}^0$

BA = BC ( chứng minh trên)

$\angle$(ABO ) = $\angle$(CBH) ( đối đỉnh)

Suy ra $∆$AOB = $∆$CHB ( cạnh huyền, góc nhọn)

⇒ CH = AO

Vì A, O cố định nên OA không đổi suy ra CH không đổi

Vì C thay đổi cách Ox một khoảng bằng OA không đổi nên C chuyển động trên đường thẳng song song với Ox, cách Ox một khoảng bằng OA.

Khi B trùng O thì C trùng với điểm K đối xứng với A qua điểm O.

Vậy C chuyển động trên tia Kz // Ox, cách Ox một khoảng không đổi bằng OA.

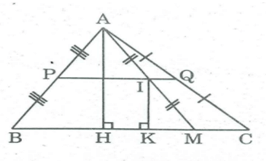
Kẻ AH ⊥ BC,IK ⊥ BC ⇒ AH // IK

Trong $∆$AHM, ta có:

AI = IM (gt)

IK // AH ( chứng minh trên)

Suy ra IK là đường trung bình của $∆$AHM

⇒ IK = 1/2 AH

$∆$ABC cố định nên AH không thay đổi ⇒ IK = 1/2 AH không đổi.

I thay đổi cách BC một khoảng bằng AH/2 không đổi nên I nằm trên đường thẳng song song với BC, cách BC một khoảng bằng AH/2

Khi M trùng với điểm B thì I trùng với điểm P là trung điểm của AB.

Khi M trùng với điểm C thì I trùng với điểm Q là trung điểm của AC.

Vậy khi M di chuyển trên cạnh BC của $∆$ABC thì trung điểm I của AM chuyển động trên đường trung bình PQ của $∆$ABC

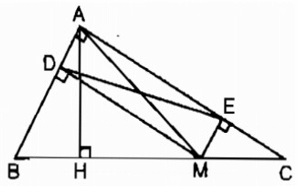
Xét tứ giác ADME, ta có:

$\angle$A = ${90}^0$ (gt)

MD ⊥ AB (gt)

⇒ $\angle$(MDA ) = ${90}^0$

ME ⊥ AC (gt)

⇒ $\angle$(MEA ) = ${90}^0$

Suy ra tứ giác ADME là hình chữ nhật ( vì có ba góc vuông)

⇒ AM = DE ( tính chất hình chữ nhật)

Ta có: AH ⊥ BC nên AM $\ge$ AH (quan hệ đường vuông góc và đường xiên)

Dấu “=” xảy ra khi M trùng với H

Mà DE = AM ( chứng minh trên)

Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC

Kẻ AK ⊥ d,BH ⊥ d

Vì M thay đổi trên d, B đối xứng với A qua M nên AM = MB

Xét tam giác vuông AKM và BHM. Ta có: $\angle$(AKM ) = $\angle$(BHM ) = ${90}^0$

AM = MB ( chứng minh trên)

$\angle$(AMK ) = $\angle$(BMH ) ( đối đỉnh)

Do đó $∆$AKM = $∆$BHM ( cạnh huyền,góc nhọn) ⇒ AK = BH

Điểm A cố định, đường thẳng d cố định nên AK không đổi.

M thay đổi, B thay đổi cách đường thẳng d cố định một khoảng bằng AK không thay đổi nên B chuyển động trên đường thẳng xy song song với d và cách d một khoảng bằng AK.