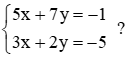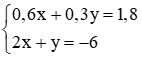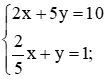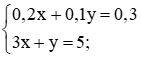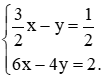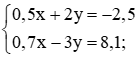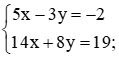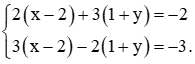Giải SGK Toán 9 KNTT Bài tập cuối chương 1 có đáp án
41 người thi tuần này 4.6 815 lượt thi 14 câu hỏi
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
32.9 K lượt thi
3 câu hỏi
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
29.1 K lượt thi
4 câu hỏi
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
7.1 K lượt thi
5 câu hỏi
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
2 K lượt thi
12 câu hỏi
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
6.2 K lượt thi
87 câu hỏi
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
2 K lượt thi
12 câu hỏi
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1
7.5 K lượt thi
5 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
Nhân hai vế của phương trình thứ nhất cho 3 và chia hai vế của phương trình thứ hai cho 5, ta được: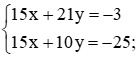 
Trừ từng vế hai phương trình của hệ mới, ta được 11y = 22 hay y = 2.
Thế y = 2 vào phương trình thứ hai của hệ đã cho, ta có 3x + 2 . 2 = –5 hay 3x = –9, suy ra x = –3.
Do đó, hệ phương trình đã cho có nghiệm là (–3; 2).
Vậy ta chọn đáp án B.
Lời giải
Đáp án đúng là: C
• Thay x = 1; y = 2 vào phương trình đường thẳng, ta có:
4 . 1 – 3 . 2 = 4 – 6 = –2 ≠ –1.
Suy ra đường thẳng 4x – 3y = –1 không đi qua A(1; 2).
Do đó, loại đáp án A và D.
• Thay x = 5; y = 6 vào phương trình đường thẳng, ta có:
4 . 5 – 3 . 6 = 20 – 18 = 2 ≠ –1.
Suy ra đường thẳng 4x – 3y = –1 không đi qua B(5; 6).
Do đó, loại đáp án B.
• Thay x = 2; y = 3 vào phương trình đường thẳng, ta có:
4 . 2 – 3 . 3 = 8 – 9 = –1.
Suy ra đường thẳng 4x – 3y = –1 không đi qua C(2; 3).
Do đó, ta chọn đáp án C.
Lời giải
Đáp án đúng là: C
Chia hai vế của phương trình thứ nhất cho 0,3 và nhân hai vế của phương trình thứ hai với 2, ta được: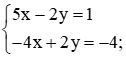 
Cộng từng vế hai phương trình của hệ mới, ta được x = −3.
Thế x = −3 vào phương trình thứ hai của hệ đã cho, ta có
(−2) . (−3) + y = –2 hay 6 + y = –2, suy ra y = –8.
Do đó, hệ phương trình đã cho có nghiệm là (−3; −8).
Lời giải
Đáp án đúng là: B
Chia hai vế của phương trình thứ nhất cho 0,3 ta được: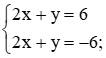 
Trừ từng vế hai phương trình của hệ mới, ta được 0x + 0y = 12. (1)
Do không có giá trị nào của x và y thỏa mãn hệ thức (1) nên hệ phương trình đã cho vô nghiệm.
Lời giải
a) Nhân hai vế của phương trình thứ nhất với 5, ta được: 
.
Trừ từng vế hai phương trình của hệ mới, ta được 0x + 0y = 5. (1)
Do không có giá trị nào của x và y thỏa mãn hệ thức (1) nên hệ phương trình đã cho vô nghiệm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.