(Đúng sai) 37 bài tập Xác suất có điều kiện (có lời giải) - Phần 1
44 người thi tuần này 4.6 1.1 K lượt thi 76 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
20.2 K lượt thi
20 câu hỏi
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
99.1 K lượt thi
126 câu hỏi
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
19 K lượt thi
15 câu hỏi
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
23.1 K lượt thi
35 câu hỏi
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
21 K lượt thi
19 câu hỏi
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
17.7 K lượt thi
7 câu hỏi
Đề ôn luyện Toán Chương 8. Một số yếu tố thống kê, xác suất và lý thuyết đồ thị (đề số 3)
2.9 K lượt thi
22 câu hỏi
237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải (P1)
35.5 K lượt thi
30 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Đoạn văn 1
Cho hai xúc xắc cân đối và đồng chất. Gieo lần lượt từng xúc xắc trong hai xúc xắc đó.
Xét các biến cố:
A: "Tổng số chấm trên hai xúc xắc bằng 5 ";
B: "Xúc xắc thứ nhất xuất hiện mặt 2 chấm".
Lời giải
Không gian mẫu có số phần từ là 36 .
Xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 5 , biết rằng xúc xắc thứ nhất xuất hiện mặt 2 chấm, là xác suất có điều kiện \({\rm{P}}(A\mid B)\). Biến cố \(A \cap B\) chỉ có 1 kết quả thuận lợi là xúc xắc thứ nhất xuất hiện mặt 2 chấm và xúc xắc thứ hai xuất hiện mặt 3 chấm nên \({\rm{P}}(A \cap B) = \frac{1}{{36}}\). Có 6 khả năng xảy ra khi xúc xắc thứ nhất xuất hiện mặt 2 chấm nên \({\rm{P}}(B) = \frac{6}{{36}} = \frac{1}{6}\). Suy ra \({\rm{P}}(A\mid B) = \frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}} = \frac{{\frac{1}{{36}}}}{{\frac{1}{6}}} = \frac{1}{6}.\)
Suy ra Đúng
Lời giải
Không gian mẫu có số phần từ là 36 .
Xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 5 , biết rằng xúc xắc thứ nhất xuất hiện mặt 2 chấm, là xác suất có điều kiện \({\rm{P}}(A\mid B)\). Biến cố \(A \cap B\) chỉ có 1 kết quả thuận lợi là xúc xắc thứ nhất xuất hiện mặt 2 chấm và xúc xắc thứ hai xuất hiện mặt 3 chấm nên \({\rm{P}}(A \cap B) = \frac{1}{{36}}\). Có 6 khả năng xảy ra khi xúc xắc thứ nhất xuất hiện mặt 2 chấm nên \({\rm{P}}(B) = \frac{6}{{36}} = \frac{1}{6}\). Suy ra \({\rm{P}}(A\mid B) = \frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}} = \frac{{\frac{1}{{36}}}}{{\frac{1}{6}}} = \frac{1}{6}.\)
Suy ra Sai
Lời giải
Không gian mẫu có số phần từ là 36 .
Xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 5 , biết rằng xúc xắc thứ nhất xuất hiện mặt 2 chấm, là xác suất có điều kiện \({\rm{P}}(A\mid B)\). Biến cố \(A \cap B\) chỉ có 1 kết quả thuận lợi là xúc xắc thứ nhất xuất hiện mặt 2 chấm và xúc xắc thứ hai xuất hiện mặt 3 chấm nên \({\rm{P}}(A \cap B) = \frac{1}{{36}}\). Có 6 khả năng xảy ra khi xúc xắc thứ nhất xuất hiện mặt 2 chấm nên \({\rm{P}}(B) = \frac{6}{{36}} = \frac{1}{6}\). Suy ra \({\rm{P}}(A\mid B) = \frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}} = \frac{{\frac{1}{{36}}}}{{\frac{1}{6}}} = \frac{1}{6}.\)
Suy ra Đúng
Lời giải
Không gian mẫu có số phần từ là 36 .
Xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 5 , biết rằng xúc xắc thứ nhất xuất hiện mặt 2 chấm, là xác suất có điều kiện \({\rm{P}}(A\mid B)\). Biến cố \(A \cap B\) chỉ có 1 kết quả thuận lợi là xúc xắc thứ nhất xuất hiện mặt 2 chấm và xúc xắc thứ hai xuất hiện mặt 3 chấm nên \({\rm{P}}(A \cap B) = \frac{1}{{36}}\). Có 6 khả năng xảy ra khi xúc xắc thứ nhất xuất hiện mặt 2 chấm nên \({\rm{P}}(B) = \frac{6}{{36}} = \frac{1}{6}\). Suy ra \({\rm{P}}(A\mid B) = \frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}} = \frac{{\frac{1}{{36}}}}{{\frac{1}{6}}} = \frac{1}{6}.\)
Suy ra Đúng
Đoạn văn 2
Cho hai đồng xu cân đối và đồng chất. Tung lần lượt từng đồng xu trong hai đồng xu đó.
Xét các biến cố:
A: "Đồng xu thứ hai xuất hiện mặt sấp ";
Lời giải
Không gian mẫu có số phần tử là 4 .
Xác suất để đồng xu thứ hai xuất hiện mặt S , biết rằng đồng xu thứ nhất xuất hiện mặt N , là xác suất có điều kiện \({\rm{P}}(A\mid B)\). Biến cố \(A \cap B\) chỉ có 1 kết quả thuận lợi là đồng xu thứ nhất xuất hiện mặt N , đồng xu thứ hai xuất hiện mặt S nên \({\rm{P}}(A \cap B) = \frac{1}{4}\). Có 2 khả năng xảy ra khi đồng xu thứ nhất xuất hiện mặt N nên \({\rm{P}}(B) = \frac{2}{4} = \frac{1}{2}\). Suy ra
\({\rm{P}}(A\mid B) = \frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}} = \frac{{\frac{1}{4}}}{{\frac{1}{2}}} = \frac{1}{2}.\)
Suy ra Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Lớp 12A có 40 học sinh, trong đó có 25 học sinh tham gia câu lạc bộ Tiếng Anh, 16 học sinh tham gia câu lạc bộ Toán, 12 học sinh vừa tham gia câu lạc bộ tiếng Anh vừa tham gia câu lạc bộ Toán. Chọn ngẫu nhiên 1 học sinh. Xét các biến cố sau:
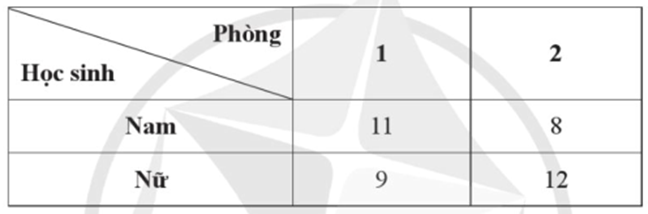
Chọn ngẫu nhiên một học sinh của lớp 12 A .
Xét các biến cố:
A: "Học sinh được chọn ở phòng 2";
B: "Học sinh được chọn là học sinh nữ".
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Một doanh nghiệp trước khi xuất khẩu mũ thời trang trong lô hàng \(X\) phải qua hai lần kiểm tra chất lượng sản phẩm, nếu cả hai lần đều đạt thì chiếc mũ trong lô hàng đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân \(96\% \) sản phẩm làm ra qua được lần kiểm tra thứ nhất và \(91\% \) sản phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qua được lần kiểm tra thứ hai. Chọn ra ngẫu nhiên một chiếc mũ thời trang trong lô hàng \(X\).
Xét các biến cố:
A: "Chiếc mũ thời trang chọn ra qua được lần kiểm tra thứ nhất";
B: "Chiếc mũ thời trang chọn ra qua được lần kiểm tra thứ hai".Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Lớp 12A có 40 học sinh, trong đó có 25 học sinh tham gia câu lạc bộ Tiếng Anh, 16 học sinh tham gia câu lạc bộ Toán, 12 học sinh vừa tham gia câu lạc bộ tiếng Anh vừa tham gia câu lạc bộ Toán. Chọn ngẫu nhiên 1 học sinh. Xét các biến cố sau:
A: “Học sinh được chọn tham gia câu lạc bộ Tiếng Anh”;
B: “Học sinh được chọn tham gia câu lạc bộ Toán”.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 6
Trong một hộp có \(18\) quả bóng bàn loại I và \(2\) quả bóng bàn loại II, các quả bóng bàn có hình dạng và kích thước như nhau. Một học sinh lấy ngẫu nhiên lần lượt \(2\) quả bóng bàn (lấy không hoàn lại) trong hộp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 7
Để nghiên cứu sự phát triển của một loại cây, người ta trồng hạt giống của loại cây đó trên hai lô đất thí nghiệm M, N khác nhau. Xác suất phát triển bình thường của cây đó trên các lô đất M và N lần lượt là 0,56 và 0,62. Lặp lại thí nghiệm trên với đầy đủ các điều kiện tương đồng. Xét các biến cố:
A: “Cây phát triển bình thường trên lô đất M”;
B: “Cây phát triển bình thường trên lô đất N”.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 9
Gieo một xúc xắc cân đối và đồng chất 1 lần. Xét các biến cố:
A: "Mặt xuất hiện của xúc xắc ghi số ";B: "Mặt xuất hiện của xúc xắc ghi số lè".
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 10
Cho hai biến cố \(A\) và \(B\) có \(P\left( A \right) = 0,4\), \[P\left( {\bar B} \right) = 0,5\], \[P\left( {A|\bar B} \right) = 0,3\]. Khi đó:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 11
Cho hai biến cố \(A\) và \(B\) có \(P\left( A \right) = 0,4\), \[P\left( B \right) = 0,4\], \[P\left( {A\bar B} \right) = \frac{3}{8}\]. Khi đó:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 12
Cho hai biến cố \(A\) và \(B\) có \(P\left( A \right) = 0,5\), \[P\left( B \right) = 0,8\], \[P\left( {AB} \right) = 0,3\]. Khi đó:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 13
Một hộp có 20 sản phẩm , trong đó có 6 sản phẩm không tốt. Lấy liên tiếp 2 sản phẩm ( sản phẩm lấy ra lần thứ nhất không bỏ lại. là biến cố lần 1 lấy được sản phẩm tốt,
là biến cố lần 2 lấy được sản phẩm tốt
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 14
Hai người độc lập rút thăm trúng thưởng. Xác suất trúng thưởng lần lượt là và
. Khi đó:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 15
Một hộp có 7 bi đỏ và 5 bi trắng. Có 5 bi được đánh số gồm 2 bi đỏ và 3 bi trắng. Lấy ngẫu nhiên 1 bi trong hộp. A là biến cố lấy được bi màu đỏ, B là biến cố lấy được bi đánh số. Khi đó
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 16
Một lớp học có 40 học sinh tương ứng số thứ tự 1 đến 40. Trong đó có 25 bạn nữ và 10 bạn nữ có số thứ tự chẵn. Chọn ngẫu nhiên 1 bạn. là biến cố chọn bạn nữ,
là biến cố chọn được bạn có số thứ tự lẻ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 17
Cho hai biến cố độc lập và
với
,
. Khi đó
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 18
Trong một lớp học, có học sinh học tốt cả Toán và Văn, có
học sinh học tốt Toán. Tính xác suất để một học sinh học tốt Văn biết học sinh đó học tốt Toán.
Gọi là biến cố: “Học sinh học tốt Văn”
Gọi là biến cố: “Học sinh học tốt Toán”.
Khi đó:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 19
Cho các biến cố và
là độc lập. Khi đó:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 20
Xét tính đúng, sai của các khẳng định sau:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập