10 bài tập Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một khoảng, đoạn hay nửa khoảng có lời giải

Đáp án đúng là: C

Xét hàm số f(x) = x³ – 3x² – 9x +10 trên đoạn [−2; 2] , ta có: f'(x) = 3x² – 6x – 9.

Có f'(x) = 0 3x² – 6x – 9 = 0 x = −1 [−2; 2] hoặc x = 3 [−2; 2]

Có f(−2) = 8; f(−1) = 15; f(2) = −12.

Suy ra \[\mathop {max}\limits_{\left[ { - 2;\,2} \right]\,} f\left( x \right) = f\left( { - 1} \right) = 15\].

Đáp án đúng là: B

Ta có \(y' = 1 - \frac{4}{{{x^2}}} \Rightarrow y' = 0 \Leftrightarrow {x^2} = 4 \Rightarrow x = 2\) (vì x (1; 5)).

Khi đó y(1) = 5; y(2) = 4 và \(y\left( 5 \right) = \frac{{29}}{5}\).

Do đó \(\mathop {\min }\limits_{\left[ {1;5} \right]} y = 4\) tại x = 2.

Đáp án đúng là: C

Hàm số đã cho liên tục trên [0; 3]

Ta có \(y' = \frac{2}{{{{\left( {x + 1} \right)}^2}}} > 0\) với ∀x [0; 3] .

Có y (0) = −1; \(y\left( 3 \right) = \frac{1}{2}\). Do đó \(\mathop {\min }\limits_{\left[ {0;3} \right]} y = y(0) = - 1\).

Đáp án đúng là: A

Ta có: y' = −2sin2x; y' = 0 sin2x = 0 \( \Leftrightarrow x = \frac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)\).

Vì x [0; π] \(x \in \left\{ {0;\frac{\pi }{2};\pi } \right\}\).

Do đó: y(0) = −2; \(y\left( {\frac{\pi }{2}} \right) = - 4;y\left( \pi \right) = - 2\).

Vậy \(\mathop {\min }\limits_{\left[ {0;\pi } \right]} y = - 4\).

Đáp án đúng là: A

Ta có: f'(x) = (2x – 5)e^2x; f'(x) = 0 \(x = \frac{5}{2}\).

Bảng biến thiên của hàm số:

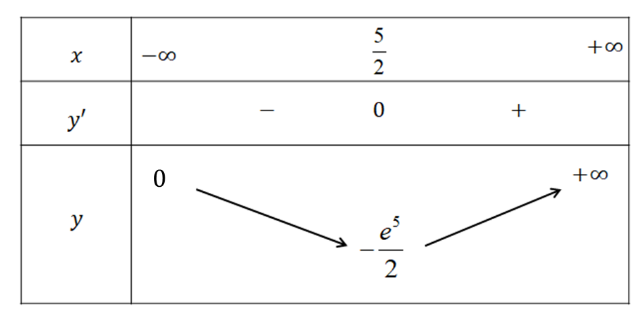
Vậy \(\mathop {\min }\limits_\mathbb{R} f\left( x \right) = - \frac{{{e^5}}}{2}\).