Bộ 20 đề thi Giữa kì 1 Toán 12 Chân trời sáng tạo có đáp án - Đề 11
25 người thi tuần này 4.6 1.3 K lượt thi 22 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
Câu 1
Lời giải
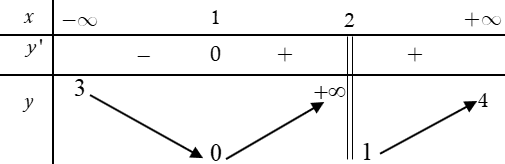
\(y' = 8{x^3} - 8x\,\,;y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\)
Bảng biến thiên:
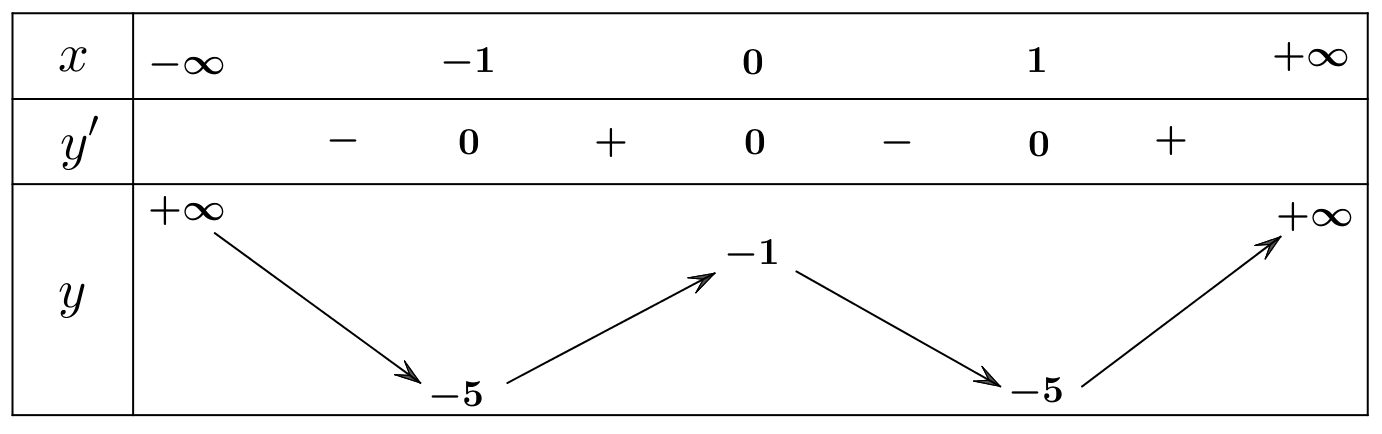
Câu 2
Lời giải
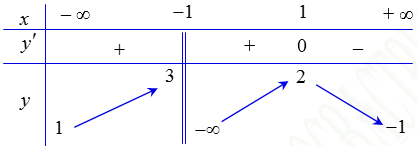
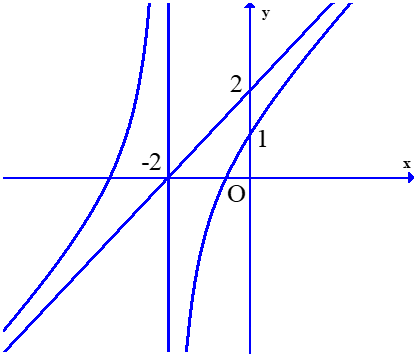
Dựa vào bảng biến thiên của hàm số ta có:
Hàm số đã cho không có đạo hàm tại điểm \(x = - 1\).
Hàm số đã cho đạt cực đại tại điểm \(x = 1\).
\(\mathop {\lim }\limits_{x \to - \infty } y = 1\), \(\mathop {\lim }\limits_{x \to + \infty } y = - 1\)nên đồ thị hàm số có hai tiệm cận ngang là các đường thẳng \(y = - 1\)và \(y = 1\).
\(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty \)nên đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 1\).
Câu 3
Lời giải
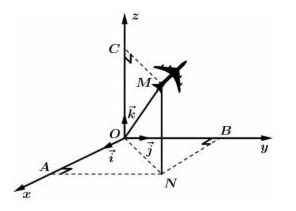
\(\overrightarrow {AB} = \left( {4; - 2; - 2} \right) \Rightarrow AB = \sqrt {16 + 4 + 4} = 2\sqrt 6 \).
Câu 4
Lời giải
Phương trình mặt cầu tâm \(I\left( {a;b;c} \right)\), bán kính \(R\) có dạng
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2} \Rightarrow {x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\left( {d = {a^2} + {b^2} + {c^2} - {R^2}} \right)\)Từ phương trình mặt cầu \(\left( S \right)\) suy ra: \(\left\{ \begin{array}{l}a = 1;b = 0;c = 0\\d = - 3\end{array} \right.\) \( \Rightarrow R = \sqrt {{a^2} + {b^2} + {c^2} - d} = 2.\)\(\)
Câu 5
Lời giải
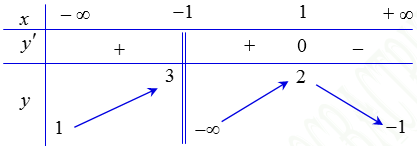
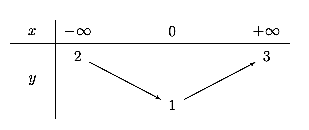
Ta có \[\left\{ \begin{array}{l}\exists x = 0:\,f\left( 0 \right) = 1\\\forall x \in \mathbb{R}:\,f\left( x \right) \ge 1\end{array} \right.\] nên \[\mathop {\min }\limits_\mathbb{R} f\left( x \right) = 1\]. Suy ra A đúng C và D sai.
B sai vì không tồn tại \[x\] để \[f\left( x \right) = 3\].
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.


![Cho một tấm bìa hình vuông có cạnh \[2m\]. Từ t (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/17-1761639676.png)