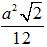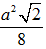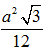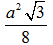6 câu Dạng 4: Xác định thiết diện chứa một đường thẳng và vuông góc với một mặt phẳng có đáp án
28 người thi tuần này 4.6 4.2 K lượt thi 6 câu hỏi 45 phút
🔥 Đề thi HOT:
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
Bài tập Giới hạn cơ bản, nâng cao có lời giải (P1)
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 1
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
20 câu trắc nghiệm Toán 11 Kết nối tri thức Mẫu số liệu ghép nhóm có đáp án
20 câu Trắc nghiệm Toán 11 Cánh diều Bài 5. Hình lăng trụ và hình hộp (Đúng-sai, trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 11 Cánh diều Bài 4. Hai mặt phẳng song song (Đúng-sai, trả lời ngắn) có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
Lời giải
Chọn B
Dựng
Ta có 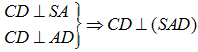
Suy ra mà suy ra
Do đó
Vì nên 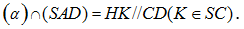
Từ đó thiết diện là hình thang ABKH
Mặt khác nên
Vậy thiết diện là hình thang vuông tại A và H
Lời giải
Chọn B
Gọi MN là đoạn thẳng qua O vuông góc AD (M, N thuộc AD, BC) ta có
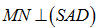 nên SMN là thiết diện cần tìm.
nên SMN là thiết diện cần tìm.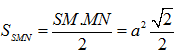
Lời giải
Chọn C
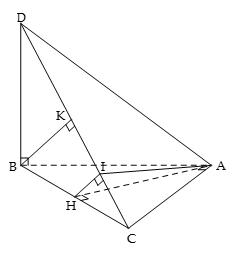
Ta có:
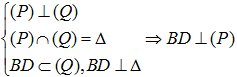
Gọi H là trung điểm BC, ta có 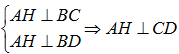
Trong mặt phẳng (BCD), kẻ 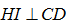 thì ta có
thì ta có 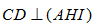
Khi đó mặt phẳng cắt tứ diện ABCD theo thiết diện là tam giác AHI
Mặt khác tam giác ABC vuông cân tại A nên 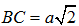
Trong tam giác vuông BCD, kẻ đường cao BK thì 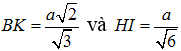
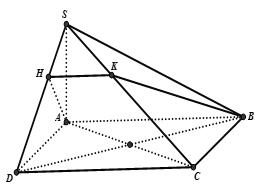
Vậy: thiết diện cần tìm là tam giác AHI vuông tại I và có diện tích 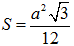
Lời giải
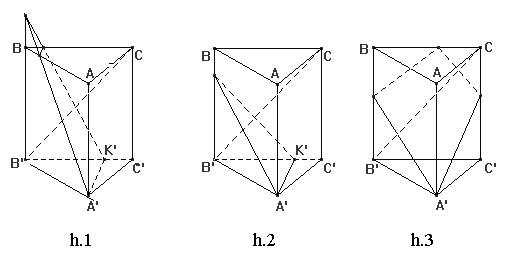
Chọn A
Gọi (P) là mặt phẳng đi qua A' và vuông góc với BC.
Từ A' ta dựng , Vì nên .
Mặt khác trong mặt phẳng (BCC'B) dựng và cắt B'B tại 1 điểm N (2) (điểm gì đề chưa có cho nên cho tạm điểm N).
Từ (1) và (2) ta có :
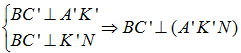
Câu 5
Lời giải
Chọn B
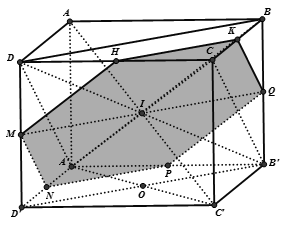
Ta có AC là hình chiếu của AC' lên (ABCD) mà 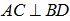 nên
nên 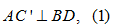
Ta có 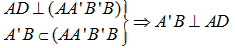
Lại có 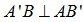 suy ra
suy ra 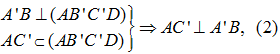
Từ (1) và (2) suy ra 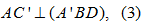
Mặt phẳng trung trực AC' là mặt phẳng đi qua trung điểm I của AC' và 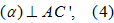
Từ (3) và (4) suy ra 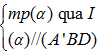
Do đó
Qua I dựng MQ // BD
Dựng

Mà 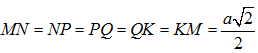
Suy ra thiết diện là lục giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
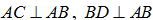 và AB = AC = BD = a
và AB = AC = BD = a