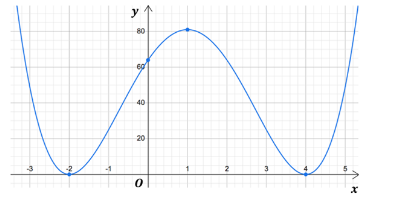
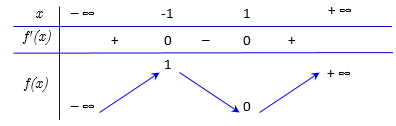
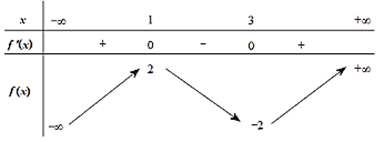
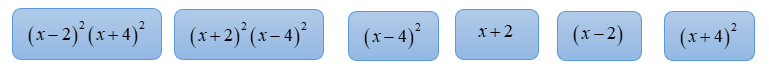Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
78 người thi tuần này 4.6 1.6 K lượt thi 100 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 3)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 15)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 14)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 13)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 12)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 11)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 10)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 9)
Danh sách câu hỏi:
Đoạn văn 1
Đọc văn bản sau và trả lời các câu hỏi từ 1 đến 10:
B-LEARNING VÀ ĐẶC ĐIỂM DẠY HỌC ĐẠI HỌC
[0] Dạy học kết hợp (BL) đang là một hình thức dạy học được nghiên cứu và triển khai rộng rãi trên thế giới. Những nghiên cứu cho thấy BL khá phù hợp với dạy học ở bậc đại học trong thời đại kỷ nguyên số.
[1] BL được xem là một dạng thức học tập kết hợp giữa học tập mặt đối mặt (F2F) và học tập trực tuyến (OL). Trong đó, dạng đơn giản nhất là kết hợp giao tiếp đối thoại trực tiếp trên lớp và tương tác gián tiếp qua môi trường mạng nhằm đạt được mục tiêu dạy học. Mặc dù định nghĩa có vẻ đơn giản, song thực tế triển khai BL phức tạp hơn nhiều. Vì vậy, điều cần thiết là phải thiết kế lại cấu trúc, cũng như cách tổ chức dạy học, sao cho đáp ứng được các nguyên tắc chủ yếu sau: Tích hợp chặt chẽ giữa F2F và OL; Thiết kế lại khóa học (nội dung, tổ chức, phương pháp…) sao cho tối ưu sự tham gia của người học; Cấu trúc lại và thay thế cách liên lạc/giao tiếp truyền thống
[2] Tích hợp chặt chẽ giữa F2F và OL không phải là sự cộng cơ học giữa 2 hình thức này, mà phải phối kết hợp với nhau theo trình tự, vừa đảm bảo được tính linh hoạt, phát huy được điểm mạnh của từng hình thức học tập, đồng thời giảm bớt sự hạn chế của chúng. Sự tích hợp này để bổ sung cho nhau. Chẳng hạn F2F rất hữu dụng cho việc giao tiếp, giải thích hay làm mẫu cần có sự tương tác giữa người và người; trong khi OL rất thuận lợi cho việc tự học, chủ động về thời gian và cần sự tự giác của người học, đồng thời đáp ứng được đào tạo với số lượng học viên lớn trong cùng thời điểm, nên tiết kiệm không gian lớp học truyền thống cũng như chi phí liên quan.
[3] Giáo dục đại học với chức năng đào tạo nguồn nhân lực chất lượng cao, có khả năng thích ứng với sự thay đổi, đáp ứng được yêu cầu của xã hội. Mặt khác, giáo dục đại học cũng hướng tới sự khai phóng, tạo điều kiện cho người học được chủ động, sáng tạo trong tư duy, học tập và làm việc với động lực và sự tự giác cao. Hình thức học tập trực tuyến rất phù hợp với những người có khả năng tự lực, tự giác và độc lập cao vì họ được giao quyền chủ động trong việc kiểm soát tiến trình học tập và có khả năng tự tìm kiếm giải pháp để giải quyết các vấn đề nảy sinh trong quá trình học tập.
[4] Với hình thức OL, để phát huy tối đa hiệu quả, khóa học trực tuyến phải được thiết kế phù hợp với khả năng người học, có sẵn các dạng tài nguyên phong phú, đồng thời có những biện pháp kịp thời hỗ trợ người học (ví dụ: diễn đàn học tập, ghi nhận những khó khăn gặp phải của người học, giải đáp thắc mắc trực tuyến….). Vì thế, để tổ chức thành công hình thức dạy học này, đòi hỏi cần sự đầu tư về nền tảng thiết bị, công nghệ và thiết kế nội dung học tập cũng như phương pháp dạy học phù hợp. Tuy vậy, thực tế cho thấy người học khác nhau về nhiều mặt: phong cách, năng lực, sở thích, kinh nghiệm, trải nghiệm học tập... Đối với hình thức học tập OL, người học còn gặp phải các vấn đề: (i) thiếu sự tương tác giữa người dạy-người học và người học với nhau; (ii) sự thiếu động lực, hứng thú khi đọc tài liệu trực tuyến và (iii) trở lực trong việc tự chủ động học tập.
[5] Chính vì vậy, BL sẽ giúp khắc phục những vấn đề tồn tại của F2F và cả OL, khi kết hợp được sự tương tác trực tiếp của người dạy trên lớp để giải đáp, khuyến khích, nhắc nhở và động viên và sự hỗ trợ cao của công nghệ với hình thức OL. Bên cạnh đó, bằng sự thay đổi phương pháp dạy học, chẳng hạn sự thay đổi tiến trình dạy học với hình thức dạy học đảo trình hay lớp học đảo, sẽ khuyến khích sự chủ động của người học tìm hiểu trước kiến thức và nhận được giải đáp, hỗ trợ phù hợp của người dạy.
[6] Những nghiên cứu đều khẳng định sự tích cực và phù hợp của hình thức dạy học BL đối với việc dạy học ở bậc đại học; tăng cường hiệu quả học tập, khuyến khích tạo ra một môi trường linh hoạt, năng động, sáng tạo và thúc đẩy sự tự học, tự nghiên cứu đối với người học. Người học có sự hài lòng, và do đó có thái độ tích cực đối với BL. Sự tham gia tích cực của họ vào quá trình học tập, vì thế sẽ có kết quả khả quan đối với các bài kiểm tra theo tiến trình, cũng như cuối khóa. Vì vậy, nghiên cứu về BL và áp dụng hình thức dạy học này ngày càng được mở rộng trên phạm vi toàn thế giới, trong đó có Việt Nam.
(Theo Vũ Thái Giang và, Nguyễn Hoài Nam, trích Dạy học kết hợp: một hình thức phù hợp với dạy học đại học ở Việt Nam thời đại kỷ nguyên số đăng trên Tạp chí nghiên cứu khoa học của Đại học Sư phạm Hà Nội, 2022.)
Câu 1
A. Có thể triển khai trên toàn bộ các bậc học, trình độ đào tạo một cách dễ dàng.
B. Tạo điều kiện cho người học và đạt hiệu quả cao trong quá trình đào tạo từ xa.
C. Khuyến khích sự tự học và tự nghiên cứu của người học trong quá trình học.
Lời giải
Đọc và tổng hợp thông tin từ đoạn [0] của bài viết: “Những nghiên cứu cho thấy BL khá phù hợp với dạy học ở bậc đại học trong thời đại kỷ nguyên số”, từ đó có thể thấy phương pháp BL dù được triển khai nhiều trên thế giới nhưng ở VN mới chỉ phù hợp với bậc đại học, khi sinh viên có khả năng tự học và đòi hỏi sự chủ động trong các vấn đề nảy sinh khi tiếp cận kiến thức, vấn đề mới.
Chọn C
Câu 2
Lời giải
Đọc và xác định thông tin trong đoạn [1] của bài viết: “BL được xem là một dạng thức học tập kết hợp giữa học tập mặt đối mặt (F2F) và học tập trực tuyến (OL). Trong đó, dạng đơn giản nhất là kết hợp giao tiếp đối thoại trực tiếp trên lớp và tương tác gián tiếp qua môi trường mạng nhằm đạt được mục tiêu dạy học.”
Chọn A
Lời giải
Đọc và xác định thông tin trong đoạn [1] của bài viết: “điều cần thiết là phải thiết kế lại cấu trúc, cũng như cách tổ chức dạy học, sao cho đáp ứng được các nguyên tắc chủ yếu sau: Tích hợp chặt chẽ giữa F2F và OL; Thiết kế lại khóa học (nội dung, tổ chức, phương pháp…) sao cho tối ưu sự tham gia của người học;”
Chọn A
Câu 4
A. Tạo ra cách kết hợp trong dạy học để thuận tiện về thời gian và không gian.
B. Tìm ra một phương pháp học tập hiệu quả, tối ưu lợi thế của từng hình thức.
C. Loại bỏ hoàn toàn sự hạn chế trong dạy học của hai phương phápF2F và OL.
Lời giải
Đọc lướt đoạn [2] và xác định nội dung của đoạn: nêu rõ rằng tích hợp giữa F2F và OL không chỉ đơn giản là cộng cơ học mà còn phải phối kết hợp hợp nhất theo trình tự để đảm bảo tính linh hoạt và tận dụng được các ưu điểm của cả hai hình thức học tập. Điều này nhằm mục tiêu tối ưu hóa trải nghiệm học tập của người học.
Chọn B
Lời giải
Đáp án
“Việc tạo ra phương pháp học tập tích hợp cần phát huy được các ưu điểm của các cách thức học tập; ví dụ như việc làm mẫu, giao tiếp của F2F hay sự chủ động về thời gian và không gian của OL nhưng vẫn cần sự cân nhắc về hiệu quả, chi phí và cách thức vận hành để có thể hoàn thành được mục tiêu đề ra.”
Giải thích
Đọc lướt câu văn cần hoàn thành và xác định nội dung nằm trong đoạn [2] của bài viết: “Chẳng hạn F2F rất hữu dụng cho việc giao tiếp, giải thích hay làm mẫu cần có sự tương tác giữa người và người; trong khi OL rất thuận lợi cho việc tự học, chủ động về thời gian và cần sự tự giác của người học, đồng thời đáp ứng được đào tạo với số lượng học viên lớn trong cùng thời điểm, nên tiết kiệm không gian lớp học truyền thống cũng như chi phí liên quan.”
Câu 6
A. Vì nó giảm bớt sự hạn chế của hình thức học tập truyền thống (F2F).
B. Vì nó tạo điều kiện cho người học được chủ động và sáng tạo trong tư duy.
C. Vì nó loại bỏ hoàn toàn sự cần thiết của người dạy trong quá trình học tập.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. Thay đổi tiến trình dạy học đảo trình.
B. Thay đổi cấu trúc và nội dung bài học.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Hỗ trợ giải quyết vấn đề nảy sinh trong quá trình học tập.
B. Khuyến khích người học tham gia vào quá trình nghiên cứu.
C. Giảm bớt lối tư duy cũ trong quá trình học tập của sinh viên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc văn bản sau và trả lời các câu hỏi từ 11 đến 20:
VƯỜN HẠCH ĐÀO
[1] […] Lý do duy nhất và cuối cùng của ông là cái chân què. Ở vùng sơn địa, sự đãi ngộ đối với nhũng người tàn phế, và những quan chức là thế này: Họ chỉ gọi họ mà không bao giờ gọi tên. La Lục Tử lại rơi vào cả hai trường hợp ấy, ở trụ sở công xã, ở trên bàn hội nghị, trước mặt ông, họ gọi ông là La bí thư, nhưng trong xóm ngõ, trong bếp núc, sau lưng ông mọi người gọi ông là La què. Nhất là trên con đường cái quan trải nhựa thẳng tắp, và hai bên đường là những hàng dương cao vút, ông từ xa đi tới, bước thước tư, bước thước bảy, mọi người chế giễu ông là đôi chân không nhất trí, và ông chê mặt đường trải lệch.
Năm năm mươi tuổi, ông bị què chân. Tám chín năm trở lại đây, cái chân què ấy có đặc dị công năng: Cứ mỗi khi trời u ám đổ mưa, cái chân lại đau, và mỗi khi đau là y như trời đổ mưa, u ám, chính xác chẳng khác gì những máy móc tinh vi. Về sau, cũng không còn chính xác lắm nữa. Bác sĩ bảo rằng nó đã trở thành bệnh tâm lý, nói đau là đau liền, nói không đau là không đau ngay tắp lự, cứ như người giả vờ ốm vậy. Khí hậu ở vùng sơn địa thay đổi thất thường, ông lo rằng cứ đau như thế và kéo dài mãi, ông đến chết mất.
— Ba mươi năm… mới đấy mà đã ba mươi năm rồi…
Ông thích xòe những ngón tay, nhớ lại những năm tháng của mình.
— Lẽ nào mà sau ba mươi năm, bố lại kéo lê cái tập tễnh ấy về quê?
Con gái, con rể ông nói thế, khiến ông im không nói gì.
Nhưng khi còn lại một mình trong nhà, ông lại thêm một lần nữa nhất quyết trở về bình nguyên Quan Trung quê cũ.
[2] Tính nết ông ương bướng, bản thân ông cũng biết rõ điều đó, nhưng không sao thay đổi đi được. Khi bà lão còn sống, thường hay ngăn cản ông, mỗi khi họp hành, ông phải báo cáo, bao giờ bà lão cũng ngồi ngay ở hàng ghế đầu. Khi thấy ông hơi hơi nổi nóng lên, nói năng đã bắt đầu quá lời, bà liền đưa mật cho ông. Ông xem chiếu bóng, phim Lâm Tắc Từ, ông rất tâm đắc với bức hoành mang hai chữ Nén Giận (Chế Nộ) treo ở trong phòng Lâm Đại Nhân, và trong một thời gian dài, ông đã từng gọi bà lão là bà Nén Giận.
Đến nay bà lão đã mất, tính nết ông không còn bị gò bó, kiểm soát nữa, cái quyết tâm trở lại bình nguyên quê cũ không còn ai có thể lay chuyển được nữa, ông bắt tay vào việc thu xếp hành trang.
[3] Đồ đạc trong nhà ông ít ỏi đến thảm hại. Ba mươi năm trước ông còn là một chàng trai tơ, từ Quan Trung lên vùng sơn địa Thương Châu, làm anh liên lạc trong ủy ban huyện. Ngày ấy công văn giấy tờ không nhiều, lại chẳng phải dậy sớm hàng ngày để lấy nước sẵn cho ông Huyện trưởng rửa ráy, hoặc phải quét dọn gì, mà chỉ có mỗi một việc là Huyện trưởng sai chạy giấy xuống các xã bằng ngựa, ông chỉ việc lo ăn lo uống cho chú ngựa là xong. Về sau ông làm nhân viên bán hàng, rồi cán sự công xã, thậm chí còn gánh vác cả công việc của Hội Phụ nữ — khi ấy cán bộ nữ còn rất ít — ông đã làm chủ nhiệm Hội Phụ nữ. Cũng trong thời kỳ ấy ông có làm quen được với một cô gái người địa phương, và từ đó cô trở thành vợ ông. Thời ấy người ta không ưa việc mua sắm đồ đạc gia đình, mãi về sau này mới có cái mốt mua sắm thêm mấy chục cái chân, nhưng thói quen của ông không thay đổi được nữa. Vì thế, trong nhà ông bây giờ, chỉ có hai chiếc hòm con con mối mọt, và chỉ trong một buổi tối ông đã thu xếp xong mọi thứ hành trang. Ông đi đến mộ vợ ông lần cuối để từ biệt bà lão, ông ngồi trước mộ bà rất lâu, sau đó ông đến vái mấy vái trước hai nấm mộ cha mẹ mình đặt phía sau ngôi mộ vợ ông.
Nhưng cô con gái và cậu con rể kiên quyết không cho ông ra đi, họ đem hai chiếc hòm nát giấu về nhà ở trên huyện.
[4] Trong thời gian còn chưa ra đi được, ông sống một mình trong một gian phòng tập thể của công xã. Mỗi khi hoàng hôn buông xuống, ông thường thích một mình ra ngồi trên một mỏm núi trước trụ sở công xã. Mỏm núi rất dốc, bên dưới là một dòng sông. Dòng sông bao quanh một khối đá tròn to như thế, nên con sóng, trước sau chỉ đập vào một nơi, không đổi thay sắc thái, lúc nào cũng chỉ là một màu trắng, không giống tuyết, cũng không giống hoa, mà nó giống như những dải giấy trắng nhỏ, dài, vo thành từng mớ, từng mớ. Không khí vùng sơn địa thật trong lành, ngồi ngắm nhìn sự đổi thay của bóng mây, dáng núi; lắng nghe tiếng âm nhạc của sông găm vào vách núi, vậy mà lòng ông rối loạn, mà chẳng tìm cho ra được đầu nào, mối nào. Những lúc như thế ông thường lần trong túi, lấy ra hai hạt hạch đào, vò vò trong tay khiến chúng vang lên những tiếng lách cách, lách cách nho nhỏ.
Hai hạt hạch đào không to, đầy những nếp nhăn dọc ngang xoắn xuýt, và ông quý mến nó, coi nó như một thứ bảo bối của mình, đi đâu ông cũng mang theo nó trong người, và khi không có việc gì, ông lại lấy nó ra vo vo trong tay, làm cho nó vang lên những tiếng lách cách, lách cách. Mồ hôi trong tay làm cho hai hạt hạch đào bóng lộn lên, và đổi thành màu nâu sậm, đến độ trông chúng chẳng còn có vẻ là hạt hạch đào nữa.
(Trích “Vườn hạch đào” – Giả Bình Ao)
Câu 11
A. Một khoản tiền lương hưu do sự đóng góp của họ cho xã hội.
B. Căn nhà 2 phòng ngủ để họ có thể sống cùng con cái của mình.
C. Gọi tên họ theo bí danh, dựa trên một đặc điểm nổi bật nào đó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. Căn nhà thiếu vắng hơi ấm của người phụ nữ do vợ ông đã mất sớm.
B. Ông nhận chức bí thư nhưng vì cái chân què mà không thể đi xa được.
C. Con cái ông không đồng ý về quê sống nên gia đình rất hay có cãi vã.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. Ông La cần uống mật khi lên báo cáo nên bà ngồi ở hàng đầu để dễ dàng đưa cho ông.
B. Bà La là người cẩn trọng, muốn ngồi ở hàng đầu để có thể theo dõi được ông khi nói.
C. Ông La là người bảo thủ và nóng giận nên bà muốn kiểm soát ông những lúc ấy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc văn bản sau và trả lời các câu hỏi từ 21 đến 26:
Chu trình nitrogen trên cạn
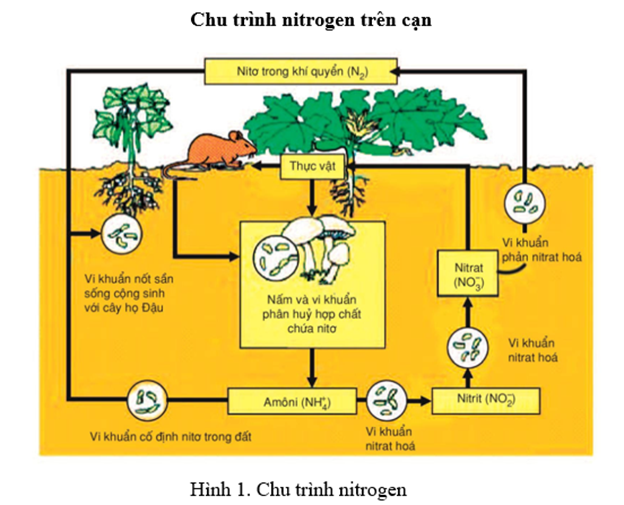
Tầm quan trọng sinh học: Nitrogen là thành phần quan trọng của các amino acid, protein, nucleic acid và thường giới hạn sinh trưởng của thực vật.
Các dạng nitrogen cần thiết cho sự sống: Thực vật sử dụng 2 dạng nitrogen vô cơ (đạm vô cơ) – ammonium (NH4+), nitrate (NO3-) và một số dạng nitrogen hữu cơ như amino acid. Hầu hết các vi khuẩn có thể sử dụng tất cả các dạng nitrogen kể cả nitrite (NO2-). Trong khi động vật chỉ sử dụng nitrogen hữu cơ.
Nguồn dự trữ nitrogen: Nguồn dự trữ nitrogen chủ yếu là bầu khí quyển, với 80% khí nitrogen (N2). Nguồn dự trữ khác là trong đất và các trầm tích hồ, sông và đại dương (nitrogen liên kết); nước bề mặt và nước ngầm (nitrogen hòa tan); và sinh khối của sinh vật sống.
Các quá trình chủ yếu: Con đường chính của nitrogen đi vào hệ sinh thái là cố định nitrogen phân tử (N2) thành dạng đạm có thể sử dụng để tổng hợp thành phần nitrogen hữu cơ. Một số phân tử nitrogen cũng có thể được cố định nhờ ánh sáng mặt trời. Các dạng phân đạm NH4+ và NO3- hình thành trong bầu khí quyển, theo nước mưa và bụi đi vào các hệ sinh thái. Quá trình ammonia hóa phân giải chất hữu cơ thành đạm ammonium (NH4+). Quá trình nitrate hóa, qua hoạt động của vi khuẩn nitrate hóa, phân giải đạm ammonia thành đạm nitrate (NO3-). Dưới điều kiện kị khí, vi khuẩn phản nitrate hóa sử dụng đạm NO3- trong quá trình trao đổi chất thay cho O2 và giải phóng N2 – quá trình này được gọi là phản nitrate hóa.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. Glutamic acid + NH4+→ Glutamine.
B. ∝-ketoglutaric acid + NH4+ → Glutamic acid.
C. NO3- → N2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. Động vật có xương sống có thể hấp thụ nhiều nguồn nitrogen như muối NH4+, NO3-.
B. Vi khuẩn phản nitrate hóa có thể phân hủy NO3- thành nitrogen phân tử N2.
C. Một số loài vi khuẩn như vi khuẩn lam có khả năng cố định nitrogen từ không khí.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc văn bản sau và trả lời các câu hỏi từ 27 đến 33:
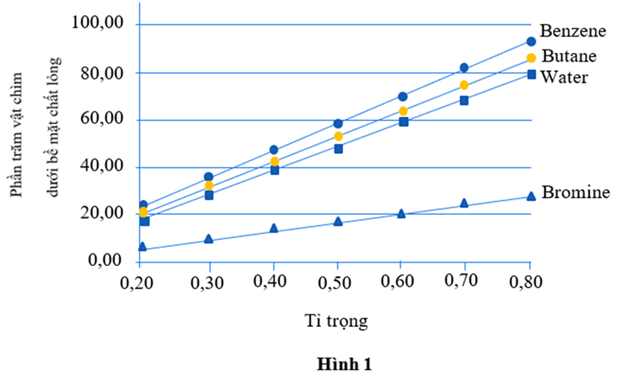
Khi một vật nổi trên bề mặt chất lỏng thì một phần của vật nằm ở phía trên bề mặt chất lỏng và phần còn lại chìm trong nước. Để nghiên cứu sự nổi của một vật có phụ thuộc vào tỉ trọng của vật không, một học sinh đã làm thí nghiệm sau:
Bảy vật (từ A đến G) có tỉ trọng khác nhau được đặt lần lượt vào trong các bình chứa 4 chất lỏng khác nhau. Tỉ trọng là tỉ lệ giữa khối lượng riêng của một vật so với khối lượng riêng của nước ở một nhiệt độ nhất định.
Bảng 1 liệt kê các vật và tỉ trọng tương ứng của chúng ở nhiệt độ 20°C.
Bảng 2 liệt kê 4 chất lỏng và tỉ trọng của chúng ở nhiệt độ 20°C.
Hình 1 cho thấy, mỗi chất lỏng tương ứng với một biểu đồ tỷ lệ phần trăm phần vật bị chìm trong chất lỏng của từng vật theo tỉ trọng của chúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. 1cm3 Bromine có khối lượng là 2,90 g.
B. 1cm3 Bromine có thể tích là 2,90 g.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. 50%
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Đọc văn bản sau và trả lời các câu hỏi từ 34 đến 39:
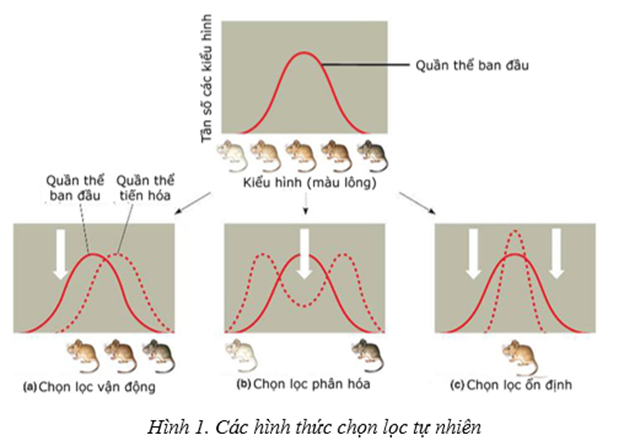
Chọn lọc tự nhiên có thể làm thay đổi sự phân bố tần số của các đặc điểm di truyền theo ba cách, tùy thuộc vào kiểu hình nào trong quần thể được chọn lọc. Ba mô hình chọn lọc này được gọi là chọn lọc vận động, chọn lọc phân hóa và chọn lọc ổn định.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
A. Trọng lượng trẻ sơ sinh vào khoảng 3 – 4 kg, những đứa trẻ có trọng lượng lớn hơn hay nhỏ hơn thì có tỉ lệ mắc bệnh, tử vong cao hơn.
B. Những con chim mỏ nhỏ sống chủ yếu bằng hạt mềm, trong khi những con chim mỏ to hơn lại sống bằng cách nghiền vỡ các hạt rắn, nên những con chim có mỏ trung bình tương đối không hiệu quả.
C. Trong một vùng đồng cỏ có phun thuốc trừ sâu, những con sâu bọ có gen quy định khả năng kháng thuốc thì được ưu tiên phát triển.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 6
Đọc văn bản sau và trả lời các câu hỏi từ 40 đến 46:
Một máy khoan dùng pin có thông số kĩ thuật như Hình 1.
|
Hình 1 |
|
Dung lượng pin |
5 Ah |
|
Điện áp định mức |
18 V |
||
|
Công suất lớn nhất |
200 W |
||
|
Mô men xoắn lớn nhất |
50 N/m |
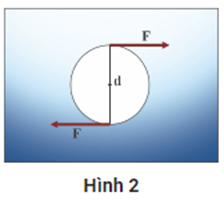
Dung lượng pin Q là lượng điện tích mà pin có thể cung cấp trong một khoảng thời gian nhất định. 5Ah có nghĩa là pin có thể cung cấp dòng điện 5 A trong 1 giờ hoặc 2,5 A trong 2 giờ. Mô men xoắn M = Fd với F là lực cắt của mũi khoan, d là đường kính lỗ khoan (bằng đường kính mũi khoan) – Hình 2.
Câu 40
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 42
Với 1 pin được nạp đầy, máy khoan có thể hoạt động với công suất tối đa trong trong bao nhiêu phút ?
Với 1 pin được nạp đầy, máy khoan có thể hoạt động với công suất tối đa trong trong bao nhiêu phút ?
A. 1,5 phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 45
A. 0,785 m/s
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 46
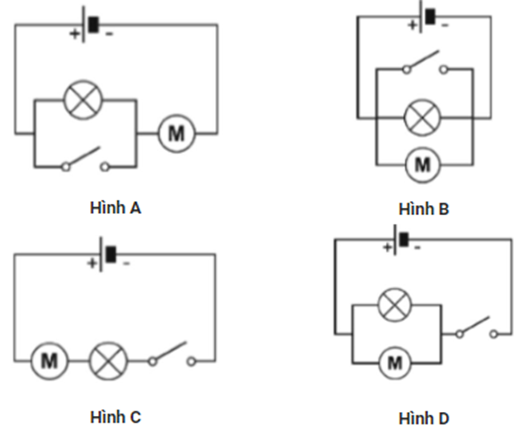
A. Hình A
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 7
Đọc văn bản sau và trả lời các câu hỏi từ 47 đến 53:
Bảng 1 liệt kê tên, công thức hóa học, khối lượng phân tử (khối lượng của 1 phân tử tính theo đơn vị khối lượng nguyên tử, amu) và nhiệt độ sôi ở áp suất khí quyển của các hợp chất khác nhau. Hợp chất đầu tiên chỉ chứa 2 nguyên tố là carbon (C) and hydrogen (H). Các hợp chất khác bao gồm carbon (C), hydrogen (H) và fluorine (F) hoặc chlorine (Cl) hoặc bromine (Br) hoặc iodine (I). Các nguyên tố F, Cl, Br và I thuộc nhóm halogen.
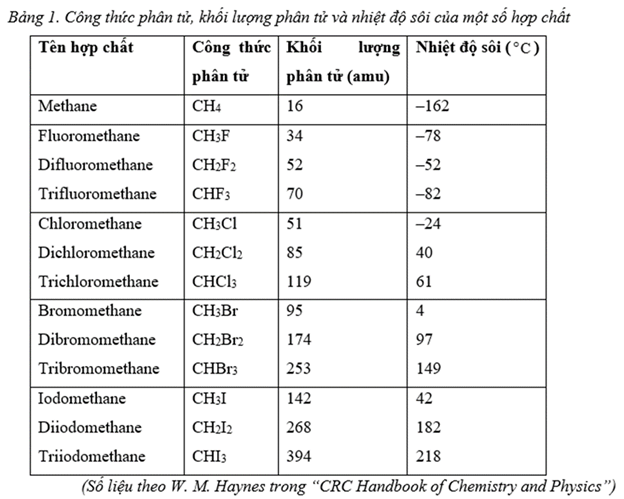
Hình 1 biểu diễn nhiệt độ sôi so với khối lượng phân tử cho 3 nhóm hợp chất (Nhóm 1-3). Mỗi hợp chất trong mỗi nhóm bao gồm C và 1 hoặc nhiều nguyên tử halogen.
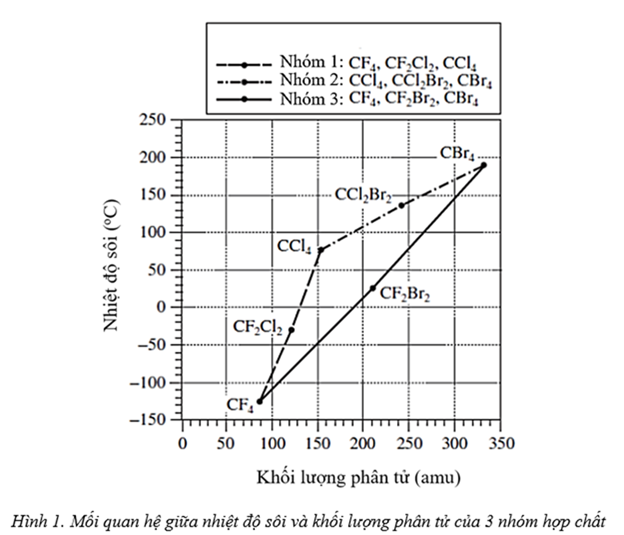
(Số liệu theo Michael Laing, "Boiling Points of the Family of Small Molecules, CHwFxClyBrz: How Are They Related to Molecular Mass?", 2001 trên American Chemical Society)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
A. CF4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. 20 amu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 8
Đọc văn bản sau và trả lời các câu hỏi từ 54 đến 60:
Để nghiên cứu cấu trúc, tính chất hoặc ứng dụng của một hợp chất hữu cơ, cần phải tách nó ra khỏi hỗn hợp, tức là tinh chế nó thành chất tinh khiết. Các phương pháp tách biệt và tinh chế thường dùng đối với chất hữu cơ là chưng cất, chiết, kết tinh và sắc kí.
1. Phương pháp chưng cất
Khi đun sôi một hỗn hợp, chất nào có nhiệt độ sôi thấp hơn sẽ chuyển vào pha hơi sớm hơn và nhiều hơn. Khi gặp lạnh, pha hơi sẽ ngưng tụ thành pha lỏng chứa chủ yếu là chất có nhiệt độ sôi thấp hơn. Quá trình đó gọi là sự chưng cất. Có các kiểu chưng cất chủ yếu sau:
a) Chưng cất thường
Khi cần tách lấy một chất lỏng có nhiệt độ sôi không cao lắm ra khỏi các chất có nhiệt độ sôi khác biệt đáng kể so với nó, người ta dùng phương pháp chưng cất đơn giản nhất gọi là chưng cất thường.
b) Chưng cất phân đoạn
Chưng cất phân đoạn dùng để tách các chất bay hơi ra khỏi một hỗn hợp dựa vào sự khác biệt về nhiệt độ sôi. Quá trình chưng cất có thể thực hiện ở áp suất khí quyển hay áp suất thấp. Phương pháp chưng cất phân đoạn được thực hiện với những bình cất có lắp cột phân đoạn và thường được nối với máy hút chân không để giảm nhiệt độ chưng cất. Nhiệt độ và áp suất được theo dõi trong quá trình chưng cất. Phương pháp này thường áp dụng để tách các chất là thành phần của tinh dầu.
c) Chưng cất dưới áp suất thấp
Khi áp suất trên mặt thoáng giảm thì nhiệt độ sôi của chất lỏng sẽ giảm theo. Vì vậy, đối với những chất có nhiệt độ sôi cao hoặc dễ bị phân huỷ ở nhiệt độ cao, cần phải chưng cất dưới áp suất thấp để giảm nhiệt độ sôi và tránh sự phân huỷ. Đối với dung môi có nhiệt độ sôi thấp như hexane, benzene, chloroform,... người ta thường dùng máy cất quay, cất ở áp suất 20 – 40 mmHg. Đối với các chất có nhiệt độ sôi cao hơn thì phải dùng bơm làm giảm áp suất xuống còn một vài mmHg. Đối với những chất sôi ở nhiệt độ cao và dễ bị tác dụng bởi nhiệt, người ta dùng phương pháp chưng cất lớp mỏng và chưng cất phân tử ở áp suất thấp tới 10–3 – 10–4 mmHg. Khi đó nhiệt độ sôi có thể giảm đi 200 – 300°C.
d) Chưng cất lôi cuốn hơi nước
Những hợp chất hữu cơ không tan hoặc rất ít tan trong nước, mặc dù có nhiệt độ sôi cao nhưng khi trộn với nước sẽ tạo ra hỗn hợp sôi ở nhiệt độ xấp xỉ 100°C (ở áp suất thường). Nhờ có một phần nước nên nhiệt độ được giữ cố định ở nhiệt độ sôi một thời gian, cũng có thể dùng áp suất cao để nâng nhiệt độ lên quá 100°C. Hơi dầu đi cùng với hơi nước vào bộ ngưng tụ và ngưng tụ lại. Hỗn hợp dầu-nước sau đó có thể tách bằng cách lắng gạn đi.
2. Phương pháp chiết
Chiết là phương pháp dùng một dung môi thích hợp hoà tan chất cần tách thành một pha lỏng (gọi là dịch chiết) phân chia khỏi pha lỏng (hoặc pha rắn) chứa hỗn hợp các chất còn lại. Tách lấy dịch chiết, giải phóng dung môi sẽ thu được chất cần tách.
3. Phương pháp kết tinh
Kết tinh dùng để tách chất rắn với chất lỏng. Dựa vào sự thay đổi độ tan theo nhiệt độ, người ta hoà tan chất cần tinh chế vào dung môi thích hợp thường là ở nhiệt độ sôi của dung môi, lọc nóng, bỏ cặn không tan rồi để nguội hoặc làm lạnh từ từ, chất rắn sẽ tách ra dưới dạng tinh thể. Lọc, rửa, làm khô sẽ thu được tinh thể chất cần tinh chế. Một chất rắn được coi là tinh khiết nếu sau nhiều lần kết tinh trong những dung môi khác nhau mà nhiệt độ nóng chảy của nó không thay đổi.
4. Phương pháp sắc kí
Phương pháp sắc kí được sử dụng để tách biệt, tinh chế và dùng trong phân tích định tính, định lượng các hỗn hợp từ đơn giản đến phức tạp. Phương pháp sắc kí dựa trên sự khác biệt về tốc độ di chuyển của các chất trong pha động khi tiếp xúc mật thiết với một pha tĩnh. Nguyên nhân của sự khác nhau đó là do khả năng bị hấp phụ và phản hấp phụ khác nhau hoặc khả năng trao đổi khác nhau của các chất ở pha động với các chất ở pha tĩnh. Có nhiều kiểu sắc kí khác nhau: Sắc kí cột, sắc kí lớp mỏng, sắc kí khí,...
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
A. Lọc và chưng cất.
B. Chiết và lọc.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
A. Chiết, chưng cất và kết tinh.
B. Chiết và kết tinh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
A. 76,125 g.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.