1. Tốt nghiệp THPT
  2. Toán
  3. Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 6: Hình học và đo lường trong không gian có đáp án

CÂU TRẮC NGHIỆM ĐÚNG SAI

33 người thi tuần này 4.6 2.8 K lượt thi 60 câu hỏi 60 phút

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

🔥 Học sinh cũng đã học

57 người thi tuần này

Đề thi thử Toán Tốt nghiệp Cụm trường QV1-TT1-LVT lần 1 năm 2026 có đáp án

114 lượt thi 22 câu hỏi
55 người thi tuần này

Đề thi thử Toán Tốt nghiệp Cụm liên trường Nghệ An lần 1 năm 2026 có đáp án

110 lượt thi 22 câu hỏi
32 người thi tuần này

Đề thi thử Toán Tốt nghiệp THCS - THPT Nguyễn Khuyến - LTT - TPHCM ngày 9-11 có đáp án

64 lượt thi 22 câu hỏi
45 người thi tuần này

Đề thi thử Toán Tốt nghiệp THPT Bãi Cháy lần 01 - Quảng Ninh năm 2025-2026 có đáp án

90 lượt thi 22 câu hỏi
24 người thi tuần này

Đề thi thử Toán Tốt nghiệp THCS - THPT Nguyễn Khuyến - LTT - TPHCM ngày 30-11 có đáp án

48 lượt thi 22 câu hỏi
111 người thi tuần này

Đề thi thử Toán Tốt nghiệp Trường THPT Đào Duy Từ - Thanh Hóa có đáp án

222 lượt thi 22 câu hỏi
84 người thi tuần này

Đề thi thử Toán Tốt nghiệp Trường THPT An Dương - Hải Phòng - Mã đề 001 có đáp án

168 lượt thi 22 câu hỏi
61 người thi tuần này

Đề thi thử Toán Tốt nghiệp Trường THPT An Dương - Hải Phòng - Mã đề 111 có đáp án

122 lượt thi 22 câu hỏi

Danh sách câu hỏi:

Đoạn văn 1

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho ba đường thẳng a, b, c phân biệt.

Câu 1

a) Nếu a song song với b thì góc giữa hai đường thẳng a và c bằng góc giữa hai đường thẳng b và c.

Lời giải

Đúng

Câu 2

b) Nếu a và b cùng song song với c thì a song song với b.

Lời giải

Đúng

Câu 3

c) Nếu a và b cùng vuông góc với c thì a song song với b.

Lời giải

Sai

Câu 4

d) Nếu a và b cùng vuông góc với c thì a vuông góc với b.

Lời giải

Sai

Đoạn văn 2

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hai mặt phẳng phân biệt \(({\rm{P}}),({\rm{Q}}).\)

Câu 5

a) Nếu \(({\rm{P}})\) và \(({\rm{Q}})\) có ít nhất một điểm chung thì \(({\rm{P}})\) và \(({\rm{Q}})\) có vô số điểm chung.

Lời giải

Đúng

Câu 6

b) Nếu \(({\rm{P}})\) và \(({\rm{Q}})\) không có điểm chung thì \(({\rm{P}})//({\rm{Q}}).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

c) Nếu \(({\rm{P}})\) chứa một đường thẳng song song với \(({\rm{Q}})\) thì \(({\rm{P}})//({\rm{Q}}).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

\({\rm{d}})\) Nếu \(({\rm{P}})\) chứa một đường thẳng vuông góc với \(({\rm{Q}})\) thì \(({\rm{P}}) \bot ({\rm{Q}}).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 3

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }.\)

Câu 9

a) Nếu ABCD là hình chữ nhật thì \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình hộp chữ nhật.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

b) Nếu \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình hộp chữ nhật thì ABCD là hình chữ nhật.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

c) Nếu \({\rm{A}}{{\rm{A}}^\prime } \bot ({\rm{ABCD}})\) thì \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình hộp đứng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

d) Nếu \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình hộp đứng thì ABCD là hình chữ nhật.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 4

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình hộp chữ nhật \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }.\)

Câu 13

a) Nếu ABCD là hình vuông thì \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình lăng trụ tứ giác đều.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

b) Nếu ABCD là hình vuông thì \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình lập phương.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

c) Nếu \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình lập phương thì \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình lăng trụ tứ giác đều.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

d) Nếu \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình lăng trụ tứ giác đều thì \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình lập phương.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 5

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình chóp \({\rm{S}}.{\rm{ABCD}}\) có ABCD là hình chữ nhật, \({\rm{SA}} \bot ({\rm{ABCD}}).\)

Câu 17

a) Số đo góc giữa hai đường thẳng SB và CD bằng số đo góc SBA.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

b) Số đo góc giữa đường thẳng SD và mặt phẳng \(({\rm{ABCD}})\) không bằng số đo góc SDA.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

c) Nhị diện \([{\rm{B}},{\rm{SA}},{\rm{D}}]\) là nhị diện vuông.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

d) Số đo góc nhị diện \([{\rm{S}},{\rm{BC}},{\rm{D}}\) ] không bằng số đo góc SBA.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 6

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho tứ diện ABCD có M, N, P lần lượt là trung điểm của các cạnh \({\rm{AB}},{\rm{BC}},{\rm{DA}};{\rm{AC}} = {\rm{BD}} = 2{\rm{a}}\), \({\rm{NP}} = {\rm{a}}\sqrt 3 .\)

Câu 21

a) \({\rm{MN}}//{\rm{AC}},{\rm{MP}}//{\rm{BD}}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

b) \(\cos \widehat {{\rm{NMP}}} = \frac{{{\rm{M}}{{\rm{N}}^2} + {\rm{M}}{{\rm{P}}^2} - {\rm{N}}{{\rm{P}}^2}}}{{2{\rm{MN}}.{\rm{MP}}}}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

c) \({\rm{MN}} = {\rm{MP}} = {\rm{a}}\sqrt 3 .\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

d) Góc giữa hai đường thẳng AC và BD bằng \({30^o}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 7

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình chóp đều \({\rm{S}}.{\rm{ABCD}}\) thoả mãn tam giác SAC vuông cân.

Câu 25

a) Số đo của góc SAC là \({45^o }.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

b) Nếu O là hình chiếu vuông góc của S trên \(({\rm{ABCD}})\) thì O là giao điểm của hai đường chéo AC và BD.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

c) Số đo góc giữa đường thẳng SA và mặt phẳng \(({\rm{ABCD}})\) bằng hai lần số đo góc SAO.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

d) Số đo góc giữa đường thẳng SA và mặt phẳng \(({\rm{ABCD}})\) bằng \({30^o }.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 8

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình chóp S.ABC có \(SA \bot (ABC),ABC\) là tam giác đều cạnh \({\rm{a}},{\rm{SA}} = \frac{{3{\rm{a}}}}{2}.\) Gọi I là hình chiếu vuông góc của A trên BC.

Câu 29

a) Đường thẳng BC không là giao tuyến của hai mặt phẳng \(({\rm{ABC}})\) và (SBC).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

b) \({\rm{SA}} \bot {\rm{BC}}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

c) Số đo góc nhị diện \([{\rm{A}},{\rm{BC}},{\rm{S}}]\) bằng số đo góc SIA.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

d) Số đo góc nhị diện \([{\rm{A}},{\rm{BC}},{\rm{S}}]\) bằng \({45^o }.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 9

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình chóp tứ giác đều \({\rm{S}}.{\rm{ABCD}}\) có \({\rm{AB}} = {\rm{a}}\), khoảng cách từ S đến mặt phẳng \(({\rm{ABCD}})\) là \(\frac{{{\rm{a}}\sqrt 3 }}{2}.\) Gọi O là hình chiếu của S trên \(({\rm{ABCD}}),{\rm{H}}\) là hình chiếu của O trên AB.

Câu 33

a) \({\rm{SO}} = \frac{{\rm{a}}}{2}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

b) Giao tuyến của hai mặt phẳng \(({\rm{SAD}})\) và \(({\rm{ADC}})\) là đường thẳng AD.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

c) \({\rm{AD}} \bot ({\rm{AHO}}).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

d) Số đo của góc nhị diện \([{\rm{S}},{\rm{AD}},{\rm{C}}]\) bằng \({30^o}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

c) \({\rm{AH}} \bot {\rm{BC}}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 10

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình chóp \({\rm{S}}.{\rm{ABC}}\) có \({\rm{SA}} \bot ({\rm{ABC}})\), \({\rm{AB}} \bot {\rm{AC}},{\rm{SA}} = 5{\rm{a}},{\rm{AB}} = 4{\rm{a}},{\rm{AC}} = 3{\rm{a}},{\rm{D}}\) là hình chiếu vuông góc của A trên \({\rm{BC}},{\rm{H}}\) là hình chiếu vuông góc của A trên SD.

Câu 38

a) \({\rm{SA}} \bot {\rm{BC}}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

b) \({\rm{BC}} \bot ({\rm{SAD}}).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

d) Khoảng cách từ A đến mặt phẳng \(({\rm{SBC}})\) là \(\frac{{60{\rm{a}}}}{{769}}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 11

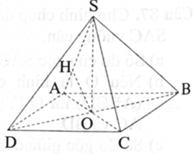
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình chóp đều \({\rm{S}}.{\rm{ABCD}}\) có \({\rm{AB}} = {\rm{a}}\), \({\rm{SA}} = 2{\rm{a}}.{\rm{O}}\) là hình chiếu vuông góc của S trên \(({\rm{ABCD}})\) H là hình chiếu vuông góc của O trên SA.

Câu 41

a) O là giao điểm của AC và BD.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

b) Hai đường thẳng BD và SO không vuông góc với nhau.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

c) Hai đường thẳng BD và OH không vuông góc với nhau.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

d) Khoảng cách giữa hai đường thẳng BD và SA là \(\frac{{{\rm{a}}\sqrt 7 }}{4}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 12

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình lăng trụ tam giác đều \({\rm{ABC}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }\) có \({\rm{AB}} = {\rm{a}}\), \(H\) là hình chiếu vuông góc của \({A^\prime }\) trên \({B^\prime }{C^\prime }.\)

Câu 45

a) \({\rm{A}}{{\rm{A}}^\prime } \bot \left( {{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }} \right).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

b) \({\rm{A}}{{\rm{A}}^\prime } \bot {{\rm{A}}^\prime }{\rm{H}}\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

c) \({{\rm{A}}^\prime }{\rm{H}} = {{\rm{A}}^\prime }{{\rm{C}}^\prime } \cdot \cos \widehat {{{\rm{A}}^\prime }{{\rm{C}}^\prime }{\rm{H}}}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

d) Khoảng cách giữa hai đường thẳng \({\rm{A}}{{\rm{A}}^\prime }\) và \({{\rm{B}}^\prime }{{\rm{C}}^\prime }\) là \(\frac{{\rm{a}}}{2}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 13

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình chóp \({\rm{S}}.{\rm{ABCD}}\) có \({\rm{SA}} \bot {\rm{SB}}\), \({\rm{SA}} = 2{\rm{a}}\), góc giữa đường thẳng SA và mặt phẳng \(({\rm{ABCD}})\) là \({60^o},({\rm{SAB}}) \bot ({\rm{ABCD}}).\) Gọi H là hình chiếu vuông góc của S trên (ABCD).

Câu 49

a) Đường thẳng AB là giao tuyến của hai mặt phẳng \(({\rm{SAB}})\) và \(({\rm{ABCD}}).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

b) SH vuông góc với mặt phẳng \(({\rm{ABCD}}).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 51

c) \(\widehat {{\rm{SAH}}} = {60^o }.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 52

d) Khoảng cách từ S đến mặt phẳng \(({\rm{ABCD}})\) bằng a.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 14

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình chóp S.ABCD có \(SA \bot SB\), ABCD là hình chữ nhật, \({\rm{AB}} = {\rm{a}},{\rm{AD}} = {\rm{b}}\), \(({\rm{SAB}}) \bot ({\rm{ABCD}}).\)

Câu 53

a) Đường thẳng AB là giao tuyến của hai mặt phẳng \(({\rm{SAB}})\) và \(({\rm{ABCD}}).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 54

b) \({\rm{AD}} \bot ({\rm{SAB}}).\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 55

c) Khoảng cách giữa hai đường thẳng SA và CD bằng b.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 56

d) Khoảng cách giữa đường thẳng CD và mặt phẳng \(({\rm{SAB}})\) bằng b.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đoạn văn 15

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hình chóp đều S.ABC có \(AB = a\), \({\rm{SA}} = {\rm{b}}.\) Gọi O là hình chiếu vuông góc của S trên mặt phẳng \(({\rm{ABC}}),{\rm{M}}\) là giao điểm của AO với BC.

Câu 57

a) Thể tích khối chóp \({\rm{S}}.{\rm{ABC}}\) được tính bằng công thức \({{\rm{V}}_{{\rm{S}}.{\rm{ABC}}}} = \frac{1}{3}\;{{\rm{S}}_{{\rm{ABC}}}}.\) SO.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 58

b) O là trọng tâm của tam giác ABC và M là trung điểm của BC.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 59

c) \({{\rm{S}}_{{\rm{ABC}}}} = \frac{1}{2}{\rm{AB}} \cdot {\rm{AC}} \cdot \cos \widehat {{\rm{BAC}}}.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 60

d) \({V_{S.ABC}} = \frac{{{a^2}\sqrt 3 }}{{12}}\sqrt {{b^2} + \frac{{{a^2}}}{3}} .\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập

Đăng ký

Bạn đã có tài khoản?