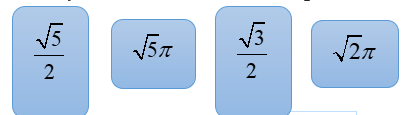Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 26)
78 người thi tuần này 4.6 1.4 K lượt thi 100 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 3)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 15)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 14)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 13)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 12)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 11)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 10)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 9)
Danh sách câu hỏi:
Đoạn văn 1
Đọc thông tin sau đây và trả lời các câu hỏi từ câu 1- câu 10:
CHIẾN THUẬT CỦA TINH TINH
[1] Tinh tinh sử dụng một chiến thuật quân sự cổ đại để ra quyết định và tránh xung đột chết chóc với đàn đối thủ, theo nghiên cứu công bố trên tạp chí PLOS Biology. Các nhà nghiên cứu phát hiện hai đàn tinh tinh miền tây (Pan troglodytes verus) ở châu Phi leo lên đồi để giám sát lẫn nhau, tương tự nhiệm vụ trinh sát trong quân đội. Sau đó, chúng sử dụng hiểu biết thu được để quyết định có nên tiến vào lãnh địa tranh chấp hay không, Live Science hôm 10/11 đưa tin.
[2] Nhiều động vật đề phòng nguy hiểm trong môi trường sống, nhưng đây là lần đầu tiên các nhà khoa học quan sát một loài không phải con người tỉ mỉ tận dụng địa thế cao để đánh giá nguy cơ trong một cuộc xung đột lãnh thổ. "Điều này thể hiện khả năng nhận thức và hành động dựa trên những gì chưa biết để thu được nhiều thông tin hơn", trưởng nhóm nghiên cứu Sylvain Lemoine, phó giáo sư nhân chủng học sinh học ở Đại học Cambridge, nhận xét.
[3] Tận dụng địa thế cao là một trong những chiến thuật quân sự cổ xưa nhất của con người trong chiến tranh, theo nhóm nghiên cứu ở Đại học Cambridge. Tinh tinh sống theo bầy đàn cạnh tranh đất đai và tài nguyên. Hành vi thông thường của chúng bao gồm phối hợp tấn công, đôi khi gây mất mạng. Lãnh thổ giữa các đàn tinh tinh không được đánh dấu bằng đá và sự hiện diện hàng ngày của chúng ở một khu vực rất quan trọng.
[4] Nghiên cứu mới theo dõi hai đàn tinh tinh sống cạnh nhau trong dự án tinh tinh Taï, một dự án bảo tồn ở vườn quốc gia Taï tại Bờ Biển Ngà. Nhóm nghiên cứu cùng với sinh viên và trợ lý người địa phương đi theo những con tinh tinh 8 - 12 giờ/ngày từ năm 2013 đến 2016, thu thập dữ liệu hành vi và GPS.
[5] Dữ liệu cho thấy tinh tinh nhiều khả năng trèo lên đồi cao hơn khi di chuyển tới ranh giới lãnh thổ của chúng. Khi ở trên đồi, chúng lặng lẽ ngồi yên thay vì tích cực làm các hoạt động có thể cản trở khả năng nghe ngóng. Những con tinh tinh trong nghiên cứu dễ di chuyển từ vùng đất cao tới lãnh thổ tranh chấp khi đối thủ ở xa, chứng tỏ chúng sử dụng ngọn đồi để tránh xung đột. Tuy nhiên, chúng cũng có thể tận dụng địa thế cao để tìm cơ hội tấn công. Lemoine để ý khi thành viên của hai đàn gặp nhau, sự cân bằng quyền lực (tức số lượng ở mỗi bên) là một yếu tố quan trọng xác định bạo lực có leo thang ở một bên hay không.
[6] Nghiên cứu của Lemoine và cộng sự chỉ xem xét tinh tinh ở vườn quốc gia Taï, nhưng họ cho rằng những con tinh tinh khác cũng sử dụng chiến thuật tương tự, tùy theo địa hình. Khả năng nhận thức phức tạp giúp tinh tinh mở rộng lãnh thổ được thúc đẩy bởi chọn lọc tự nhiên, chứng tỏ chiến thuật chiến đấu trên có nguồn gốc từ tiến hóa.
(An Khang, Báo điện tử VN Express, vnexpress.net, ngày 12/11/2023)
Lời giải
Đáp án
Một cuộc nghiên cứu về tinh tinh miền tây ở châu Phi đã hé lộ rằng chúng khôn khéo sử dụng chiến thuật quân sự cổ xưa của con người để tránh xa các cuộc đụng độ đầy nguy hiểm. Thay vì thụ động, chúng đặt mình ở vị trí cao để cảm nhận và đánh giá tình hình xung quanh, một chiến thuật mà con người từng sử dụng trong quân sự cổ đại.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
- [Vị trí thả 1]: đụng độ -> sự xung đột lực lượng hai bầy tinh tinh khi tiếp cận ranh giới lãnh thổ.
- [Vị trí thả 2]: quân sự -> thuật ngữ liên quan đến quân đội, chiến thuật được chuẩn bị để thực hiện chiến tranh hay bảo vệ; trong bài đọc là chiến thuật quân sự của con người cổ đại.
Câu 2
A. Tinh tinh thường tránh địa thế cao trong cuộc xung đột
B. Tinh tinh sử dụng chiến thuật quân sự để bảo vệ lãnh thổ.
C. Tinh tinh hiếm khi thể hiện sự nhận thức về môi trường xung quanh.
Lời giải
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [3]: “Tận dụng địa thế cao là một trong những chiến thuật quân sự cổ xưa nhất của con người trong chiến tranh, theo nhóm nghiên cứu ở Đại học Cambridge.”
=> Đáp án cần chọn là B.
Lời giải
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [6]: “Khả năng nhận thức phức tạp giúp tinh tinh mở rộng lãnh thổ được thúc đẩy bởi chọn lọc tự nhiên, chứng tỏ chiến thuật chiến đấu trên có nguồn gốc từ tiến hóa.”
=> Thông tin Đúng.
Câu 4
A. Tác giả viết bài văn trên để trình bày kết quả chi tiết một cuộc nghiên cứu về hành vi của tinh tinh.
B. Tác giả viết bài để phản đối và bác bỏ những nghiên cứu trước đó về hành vi của tinh tinh.
C. Tác giả mô tả các chiến thuật quân sự của tinh tinh nhằm tăng cường sự hiểu biết về tương tác xã hội và sinh học của chúng.
Lời giải
Phương pháp giải
Đọc hiểu nội dung toàn bài, suy ra mục đích của tác giả.
Lời giải
A đúng - Căn cứ nội dung toàn bài, bài viết trình bày kết quả của cuộc nghiên cứu về tinh tinh của nhóm nghiên cứu Đại học Cambridge.
B sai - Tác giả không có thái độ phản đối và bác bỏ với những nghiên cứu tương tự trước đó.
C đúng - Căn cứ nội dung toàn bài, suy ra mục đích sau cùng của tác giả là cung cấp thông tin cho nghiên cứu sinh học.
D sai - Bài viết không đề cập đến lịch sử và không đi sâu vào đặc điểm tự nhiên của bầy tinh tinh Bờ Biển Ngà.
=> Đáp án cần chọn là A và C.
Lời giải
Đáp án: "nhận thức"
Phương pháp giải
Xét logic câu từ và thông tin có được sau bài đọc.
Lời giải
Căn cứ nội dung đoạn toàn bài; “nhận thức” xuất hiện trong đoạn [2] và [6]. -> Khả năng nhận thức của tinh tinh trong các chiến thuật chiến đấu.
=> Từ cần điền là nhận thức.
Câu 6
A. Chiến thuật của tinh tinh không thay đổi tùy thuộc vào số lượng cá thể trong mỗi bên.
B. Các nhà nghiên cứu đã thu thập dữ liệu hành vi của bầy tinh tinh trung bình 10 giờ mỗi ngày trong suốt 3 năm.
C. Đàn tinh tinh không đánh dấu lãnh thổ mà trực tiếp có mặt để bảo vệ tài nguyên đất đai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. Chúng ta hiểu rõ hơn về sự nguy hiểm của tinh tinh trong môi trường sống tự nhiên.
B. Chiến thuật quân sự là một khía cạnh quan trọng của hành vi động vật.
C. Nghiên cứu chỉ chứng minh sự giống nhau giữa tinh tinh và con người trong chiến thuật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc thông tin sau đây và trả lời các câu hỏi từ câu 11- câu 20:
CHUYẾN BAY
[0] Trong đời một con người, dù là cả một đời bằng phẳng, tẻ nhạt thì cũng có lúc được chứng kiến những điều tưởng không thể nào giải thích nổi.
Từ bảy nhăm (1975), tôi chỉ có dịp may được ra vào thành phố Hồ Chí Minh khoảng vài ba lần. Lần cuối cùng cách đây cũng đã nhiều năm. Hình như có việc hội họp gì đấy. Tôi chẳng bao giờ là một người quan trọng. Tính tôi lại lười, kể cả lười họp lẫn lười đi chơi. Vả lại trong túi không có sẵn tiền.
[1] Tôi sống ở thành phố Hồ Chí Minh một tuần lễ hoặc dăm hôm gì đó, khuôn mình trong khách sạn bù khú với mấy người bạn và thỉnh thoảng đáo qua phòng họp rồi leo lên máy bay về Hà Nội.
Máy bay cất cánh ở sân bay Tân Sơn Nhất lúc 9 giờ sáng. Hôm ấy là một ngày nắng đẹp.
Chuyến bay của chiếc IL19.
Tôi ngồi cạnh anh bạn ở hàng ghế bên trái.
[2] Các hàng ghế bên phải và bên trái chung quanh chúng tôi đã có khách lên ngồi kín hết mới thấy một cô bé mặc bộ đồ vàng khoác chiếc túi trắng ngơ ngác, sợ sệt đi giữa hai hàng ghế, từ phía đuôi máy bay đi lên. Cô gái trạc 16, 17 tuổi là cùng. Nom kiểu người thành phố nhưng thiếu bạo dạn, lại có vẻ yểu tướng. Thấy bên cạnh tôi còn một chiếc ghế chưa có ai ngồi, cô rụt rè đi đến.
- Cháu ngồi đây được không thưa chú?
- Được, được, cô ngồi đi.
Tôi nói và dập tắt điếu thuốc.
- Chú cứ hút…
Chúng tôi làm quen với nhau khá nhanh.
Thấy tôi cũng là người thật thà, cô bé tỏ ra cởi mở. Chuyến bay cất cánh chậm 30 phút. Trước khi bay, tôi đã kịp nghĩ rằng cô bé thật là một con chim non đang bay vào đời, bay lẻ chiếc một mình mà chưa hề biết cuộc đời thực lắm nanh vuốt và trắc trở.
Tôi được biết cô bé sinh ở Lạng Sơn, sống với bố mẹ ở đấy đến bảy nhăm (1975) thì cả nhà dọn về nửa quê hương ở trong này. Cô thực ra cũng chả còn là một cô bé như tôi nghĩ. Cô đã học xong lớp 12 từ năm kia, đã trượt đại học hai năm và bây giờ ra Hà Nội để chuẩn bị đi xuất khẩu lao động ở Tiệp Khắc.
- Sắp tới đây ra Hà Nội cháu ở đâu?
- Người ta mách nên trọ ở khách sạn Đường Thành.
- Cháu đã sống ở Hà Nội bao giờ chưa?
- Thưa chú, chưa, cháu mới có dịp đi qua hồi cháu còn nhỏ, lâu rồi, ngày ở Lạng Sơn dời nhà vào…
Tôi đâm lo cho cô bé. Tôi nhìn thấy trước, cô bé sẽ bị lừa đảo, mất trộm hoặc bị cướp giật ngay giữa thủ đô Hà Nội. Tôi đang nghĩ ra một cách gì giúp cô bé…
[3] Trong lúc ấy tôi bỗng nhìn thấy ở dãy ghế bên phải có một khuôn mặt quen. Đấy là một người đàn ông. Tôi vốn kém sáng dạ, ý nghĩ chậm chạp. Hiện ra đầu tiên là thấy anh ta không mặc quân phục như ngày trước. Khuôn mặt già đi ít nhiều nhưng vẫn còn đẹp, và bây giờ tôi nhìn thấy có cái gì ác ác mà trước kia thời gian chưa kịp chạm trổ rõ hết đường nét. Có lẽ nó nằm ở đôi mắt. Đôi mắt như vẽ, có một cái nhìn chằm chặp lúc nào cũng hướng thẳng về phía trước. Hai tay người đàn ông đặt trước bụng, không hề động đậy, hơi cứng nhắc.
Toàn thân cũng thẳng đơ, như một bức tượng người sống được đặt và chèn kỹ trong chiếc ghế máy bay.
Cái tư thế ngồi ấy, hai con mắt ấy và toàn bộ con người ấy toát ra một vẻ kiêu hãnh, khiến tôi hết sức khó chịu, đầy ác cảm. Tôi đâm sợ cái người quen thuộc này trong một lúc vô tình tự phá vỡ cách sống của mình, một cách sống định hình từ cách đây rất nhiều năm.
Giống như một tảng ximăng chết, ngồi bất động bất di bất dịch, tôi sợ người đàn ông đưa mắt nhìn ngang nhìn ngửa ra hai bên, ra xung quanh, và bất ngờ nhận ra tôi.
[4] Anh ta sẽ làm gì nhỉ? Biết đâu đấy cái bức tượng đã được chèn kỹ trong chiếc ghế máy bay ấy sẽ nhổm dậy, đưa một bàn tay ra sau giữ cho cái mặt ghế khỏi sập mạnh xuống có thể gây chấn động đến những người ngồi hai bên, rồi đi đến sau lưng tôi, không, không đâu, nghĩ như thế là tôi đã nhầm đấy, từ lúc nãy tới giờ, anh ta có quay ngang quay ngửa hay động đậy cái cổ hoặc liếc mắt nhìn ai đâu.
Một con người như anh ta, tôi vẫn còn nhớ, chỉ nhìn thấy một cái ở trước mặt, luôn luôn ở trước mặt là mục đích đi tới và quyết tâm thực hiện mọi giá…
Tôi bỗng nhớ lại một buổi trưa Sài Gòn đến điếc tai vì tiếng xe gắn máy. Một ngày đầu tháng 5 bảy nhăm, một cậu liên lạc của phòng chính trị đưa xuống nhà khách sư đoàn chỗ chúng tôi đang ở, một vị sư nữ già, có lẽ trạc đã gần 60 tuổi, mặc chiếc áo dài màu nâu, may bằng thứ vải thô mà những vị tu hành ở ngoài miền Bắc cũng không còn mấy ai mặc, có chăng chỉ những vị sư trụ trì ở chùa.
[5] Máy bay cất cánh được một lúc, cô bé đã gục đầu xuống một cuốn sách, nhìn qua vai cô tôi mới nhận thấy một người đàn bà ngay từ đầu đã ngồi cạnh người đàn ông. Chẳng cần tinh đời lắm cũng đoán được người đàn bà trước đây vốn là loại người sang, quý phái là khác, nhưng trải qua một trận xáo trộn đời sống đã làm cho con người dầu dãi, nhầu nát đi.
Dưới chân người đàn bà xếp hai chiếc túi, phô trương sự giàu có. Một chiếc bị cói và một chiếc túi vải màu đỏ chói chang. Cả hai đều chứa đồ đạc đến căng ra. Trên miệng chiếc túi cói vắt một chiếc áo khoác ngắn màu cỏ úa loại thật sang của đàn ông. Người đàn bà đã khiến tôi trở nên tò mò!
Chốc chốc bà ta lại cúi xuống lôi từ chiếc túi ngực của chiếc áo khoác ra một bao thuốc lá ba con năm, rút một điếu đem cắm lên miệng người đàn ông rồi bật chiếc bật lửa ga màu xanh cho xòe lửa, châm vào đầu điếu thuốc. Con mắt đẹp nhìn chằm chằm ra phía trước và toàn thân người đàn ông ở bên cạnh vẫn bất động, chỉ thấy ở khóe miệng thỉnh thoảng nhả ra một bụm khói thuốc lá thơm. Sau đó, người đàn bà trườn mình qua trước bụng người đàn ông, bằng hai tay cầm bao ba con năm với một điệu bộ hơi khúm núm dâng lên trước một người thanh niên ngồi sát khuôn cửa sổ tròn của máy bay.
Anh thanh niên nói khẽ: “Cảm ơn”, đồng thời giơ một bàn tay xua xua trước cử chỉ mời mọc.
[6] Người thanh niên mặc quần áo vàng, đội mũ cát vàng đính phù hiệu công an. Trên thắt lưng to bản đeo bao súng ngắn, lại thêm một khẩu tiểu liên cầm lăm lăm trong tay.
Thế là tôi hiểu ra tất cả. Khi chợt nhìn thấy một chiếc còng số 8 trên hai cổ tay chắp trước bụng người đàn ông. Thảo nào!
[7] Tôi cũng đóng vai trò đồng hành với ba con người ở dãy ghế kia trong suốt hai tiếng rưỡi đồng hồ, thời gian đủ để cho tôi nhớ lại được tất cả về cái người đàn ông điển trai ngồi bất động như một bức tượng, thậm chí tôi còn nhớ được cả tên, cả giọng nói của hắn.
Riêng tôi không khỏi cảm thấy một cái gì sững sờ, thật cay đắng, thật đau xót…
(Nguyễn Minh Châu, Tuyển tập truyện ngắn Nguyễn Minh Châu, NXB Văn học, 2018)
Câu 11
A. Sự đối mặt với quá khứ.
B. Sự đồng cảm và lo lắng.
C. Sự đổi thay của tính cách con người.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. Quân phục và dây chuyền vàng
B. Đồng phục công an và bảng hiệu
C. Áo vàng, mũ cát vàng, không đeo đồ trang sức
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. Chú trọng miêu tả cảnh vật và trần thuật bên ngoài câu chuyện.
B. Tập trung vào nhân vật và các mối quan hệ giữa người với người.
C. Đề cao khía cạnh nhân văn trong mối quan hệ con người.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc thông tin sau đây và trả lời các câu hỏi từ câu 21- câu 27:
TIÊU HÓA Ở ĐỘNG VẬT
Ở các loài thú, có loài ăn thực vật, có loài ăn thịt, có loài ăn tạp (vừa ăn thực vật, vừa ăn động vật). Cho dù là sử dụng nguồn thức ăn nào thì cấu tạo của cơ quan tiêu hóa đều phù hợp với nguồn thức ăn để tối ưu hóa hiệu quả tiêu hóa.
Động vật ăn thịt: Đối với động vật ăn thịt, thức ăn rất giàu dinh dưỡng, dễ tiêu hóa cho nên cấu tạo cơ quan tiêu hóa có những đặc điểm đặc trưng: Răng phân hóa thành răng cửa, răng nanh, răng ăn thịt và răng hàm, răng cửa lấy thịt ra khỏi xương, răng nanh cắm vào con mồi và giữ mồi, răng ăn thịt rất phát triển, có chức năng xé thịt thành những miếng nhỏ, răng hàm kém phát triển; khớp hàm và cơ thái dương lớn tạo ra chuyển động lên xuống, giúp ngậm miệng giữ chặt con mồi. Ống tiêu hóa nhỏ, ngắn, dạ dày đơn có khả năng co giãn lớn, manh tràng kém phát triển.
Động vật nhai lại (trâu, bò, dê, cừu, hươu, nai): Thức ăn là thực vật, dễ kiếm, nhưng nghèo dinh dưỡng và khó tiêu hóa thì cơ quan tiêu hóa có đặc điểm: Ăn nhanh và nhiều. Răng thích hợp với giật cỏ và nghiền thức ăn: Hàm trên có tấm sừng thay cho răng cửa và răng nanh. Hàm dưới có răng cửa và răng nanh giống nhau, có tác dụng tì cỏ vào tấm sừng hàm trên, có khoảng trống không răng tạo điều kiện cho chuyển động của cỏ. Răng trước hàm và răng hàm có các gờ xi măng nổi trên bề mặt, làm tăng hiệu quả nghiền nát thức ăn. Khớp hàm, cơ cắn và cơ bướm giữa phát triển làm cho hàm chuyển động sang hai bên có tác dụng trong nhai, nghiền cỏ. Dạ dày 4 túi (Dạ cỏ, dạ tổ ong, dạ lá sách và dạ múi khế). Dạ cỏ có chứa hệ vi sinh vật phân giải xenlulô và chuyển hóa thành protein. Ruột rất dài, manh tràng phát triển và cũng có hệ vi sinh vật cộng sinh.
Động vật ăn thực vật có dạ dày đơn (ngựa, thỏ ... ): Mặc dù không chuyên hóa cao như động vật nhai lại nhưng chúng vẫn có những đặc điểm thuận lợi cho việc tiêu hóa xenlulôzơ, đó là: Dạ dày có kích thước lớn, ở giữa có eo thắt, chia dạ dày làm hai ngăn, ngăn phía trên (giáp với thực quản) không có dịch vị, tạo điều kiện thuận lợi cho các vi sinh vật phân giải xenlulô hoạt động. Ruột dài, manh tràng phát triển. Khi ăn, chúng thường nhai kĩ hơn trâu bò. Một số loài như thỏ, do hiệu quả tiêu hóa không cao nên chúng có tập tính tiêu hóa lại, thức ăn sau khi đi qua ống tiêu hóa, tiếp tục được ăn trở lại và tiêu hóa thêm một lần nữa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. Trâu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. Trâu.
B. Bò.
C. Báo đốm.
D. Ngựa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. Hàm trên có tấm sừng thay cho răng cửa và răng nanh.
B. Răng ăn thịt rất phát triển.
C. Hàm dưới có răng cửa phát triển hơn răng nanh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. Dạ dày đơn.
B. Ruột ngắn và mạnh tràng phát triển.
C. Hệ vi sinh vật cộng sinh phát triển.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc thông tin sau đây và trả lời các câu hỏi từ câu 28- câu 34:
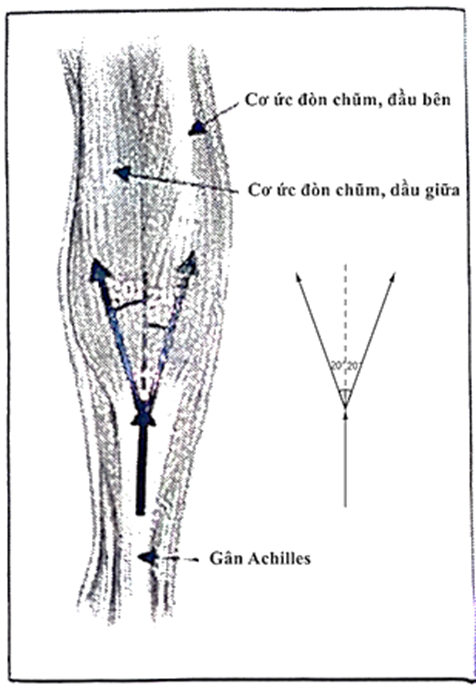
Để chuẩn bị cho giải bóng đá, một số câu lạc bộ đã thực hiện nghiên cứu để tính lực căng đặc hiệu (lực căng tối đa trên một đơn vị diện tích) của cơ bắp chân trên một trong những cầu thủ giỏi nhất của họ. Đầu tiên, họ ghi lại một số dữ liệu giải phẫu như sau:
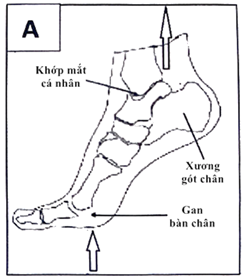
Cho biết:
- Khối lượng cơ thể của cầu thủ là 72kg.
- Diện tích mặt cắt ngang bắp chân (trung bình) là 23,0 cm2
- Khoảng cách từ gan bàn chân tới khớp cổ chân là 13,5 cm
- Khoảng cách từ xương gót chân đến khớp cổ chân là 5,20 cm
Có thể quan sát số liệu trên hình B:
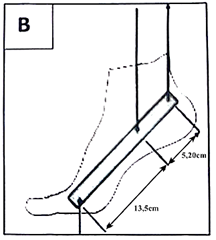
Lực căng đặc hiệu: một cầu thủ được yêu cầu nâng người lên cao nhất có thể để giữ thăng bằng trên gan của bàn chân trong hình A.
Câu 28
A. 1,35.103N
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
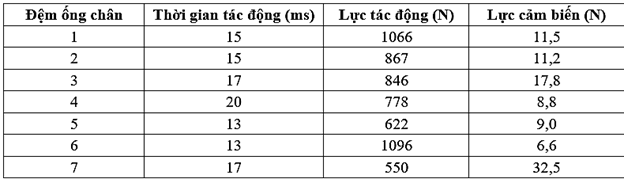
Câu 34
A. 6 – 1 – 2 – 3 – 5 – 4 - 7
B. 6 – 1 – 3 – 5 – 4 – 7 - 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Đọc thông tin sau đây và trả lời các câu hỏi từ câu 35- câu 40:
NĂNG LƯỢNG HOẠT HÓA CỦA MỘT PHẢN ỨNG HÓA HỌC
Năng lượng hoạt hóa (Ea) là năng lượng tối thiểu mà các chất phản ứng cần có để một phản ứng hóa học có thể xảy ra.
Để phản ứng hóa học xảy ra thì các phân tử các chất phản ứng phải va chạm vào nhau. Nhưng không phải mọi va chạm đều gây ra phản ứng, mà chỉ những va chạm có hiệu quả mới gây ra phản ứng. Các va chạm có hiệu quả thường xảy ra giữa các phân tử có năng lượng đủ lớn (phân tử hoạt động). đó là năng lượng dư so với năng lượng trung bình của tất cả các phân tử.
Năng lượng hoạt hóa càng lớn, số phân tử hoạt động càng ít, số va chạm có hiệu quả càng nhỏ, dẫn đến tốc độ phản ứn càng nhỏ và ngược lại, năng lượng hoạt hóa càng nhỏ, tốc độ phản ứng càng lớn.
Mối liên hệ giữa nhiệt độ, năng lượng hoạt hóa với hằng số tốc độ phản ứng được biểu thị trong phương trình kinh nghiệm Arrhenius (A-re-ni-ut):
\(k = A.{e^{\frac{{{E_a}}}{{RT}}}}\)
Trong đó:
A là hằng số đặc trưng cho mỗi phản ứng
e = 2,7183
R là hằng số khí lí tưởng (R = 8,314 J/mol.K)
T là nhiệt độ (theo thang Kelvin)
Ea là năng lượng hoạt hóa, đơn vị J/mol
Tại nhiệt độ T1 và T2 tương ứng với hằng số tốc độ và , phương trình Arrhenius được viết như sau: \(\ln \frac{{{k_{{T_2}}}}}{{{k_{{T_1}}}}} = \frac{{{E_a}}}{R}.\left( {\frac{1}{{{T_1}}} - \frac{1}{{{T_2}}}} \right)\)
Chất xúc tác làm giảm năng lượng hoạt hóa của phản ứng nên làm tăng tốc độ phản ứng hóa học. Chất xúc tác không bị biến đổi về lượng và chất sau phản ứng.
Câu 35
A. 5,87.10−4 L/mol.s.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
A. 0,082.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 40
A. Khi tăng nhiệt độ của phản ứng thì tốc độ phản ứng tăng.
B. Khi giảm nhiệt độ của phản ứng thì tốc độ phản ứng giảm.
C. Tăng nhiệt độ của phản ứng làm giảm năng lượng hoạt hóa của phản ứng nên làm tăng tốc độ phản ứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 6
Đọc thông tin sau đây và trả lời các câu hỏi từ câu 41- câu 47:
SỰ ĐIỀU HÒA HOẠT ĐỘNG GEN Ở SINH VẬT NHÂN THỰC
Ở sinh vật nhân thực, điều hòa hoạt động gen có nhiều cấp độ khác nhau, trong đó điều hòa trước phiên mã là hình thức điều hòa ít tốn kém năng lượng. Điều hòa trước phiên mã được thực hiện thông qua cơ chế điều hòa mức độ xoắn của NST. Các gen nằm trong vùng co xoắn (vùng dị nhiễm sắc) của NST sẽ không được biểu hiện. Chỉ những gen nằm trong vùng giãn xoắn (vùng nguyên nhiễm sắc) mới có cơ hội được biểu hiện. Vì thế, tế bào có thể điều hòa sự biểu hiện của gen bằng cách co, giãn xoắn NST. Quá trình này được thực hiện thông qua hai cơ chế chủ yếu: Cải biến histone và methyl hóa ADN.
- Cải biến histone: Histone tham gia cấu tạo nên nuclêôxôm, đơn vị cấu trúc của NST. Sự cải biến cấu trúc của histone có thể ảnh hưởng đến trạng thái co, giãn của NST:
+ Sự gắn nhóm acetyl vào các phân tử lysine tích điện dương của đuôi histone sẽ làm giãn xoắn NST, khởi động quá trình phiên mã của gen.
+ Sự gắn nhóm methyl vào histone sẽ làm co xoắn NST, ức chế sự biểu hiện của gen. Tuy nhiên, sự gắn nhóm photphat vào các axit amin trên phân tử histone đã được methyl hóa sẽ làm cho các vùng NST đang co xoắn giãn xoắn trở lại.
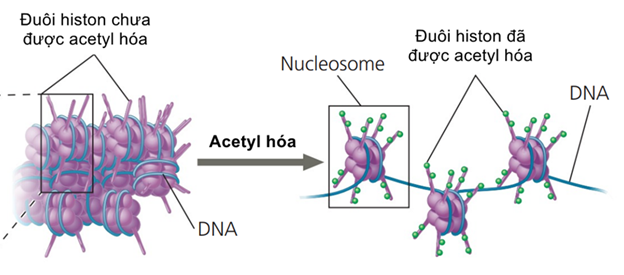
Hình 1. Quá trình Acetyl hóa đuôi histone (Nguồn: Campbell, Reece)
- Methyl hóa ADN: Sự gắn nhóm methyl vào các bazơ nitơ nhất định cũng gây ức chế hoạt động của gen. Ví dụ, khi nhóm methyl được gắn vào các bazơ xitôzin sẽ làm bất hoạt gen. Sự methyl hóa ADN thường gây ra sự bất hoạt gen trong thời gian dài, liên quan đến quá trình biệt hóa tế bào. Một điều đáng chú ý là một gen khi đã bị methyl hóa thì trạng thái methyl hóa sẽ được truyền lại cho các thế hệ tế bào con, hiện tượng này gọi là hiện tượng in vết hệ gen.
Câu 41
A. Trước phiên mã.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 43
A. Các gen nằm trong vùng dị nhiễm sắc của NST không được biểu hiện.
B. Các gen nằm trong vùng dị nhiễm sắc của NST sẽ được biểu hiện.
C. Các gen nằm trong vùng nguyên nhiễm sắc của NST không được biểu hiện.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 44
A. Sự gắn nhóm methyl vào histone.
B. Sự gắn nhóm photphat vào các axit amin trên phân tử histone.
C. Sự gắn nhóm methyl vào các bazo nito.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 46
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 7
Đọc thông tin sau đây và trả lời các câu hỏi từ câu 48- câu 54:
Trong thông tin liên lạc, để thu được tín hiệu vô tuyến, ví dụ như từ các đài vô tuyến AM/FM, cần một anten vô tuyến. Có loại anten để phát sóng cũng như có loại dùng để thu sóng. Trên đường truyền, nếu sóng điện từ gặp anten thu thì nó tạo ra một dòng điện cảm ứng biến thiên cùng tần số với sóng điện từ đó. Khi đó, một phần năng lượng của từ trường biến thành năng lượng của dòng điện cảm ứng xuất hiện trong anten thu. Anten thu thông thường là loại cảm ứng từ mạnh với thành phần điện trường \(\overrightarrow E \) của sóng điện trường. Cũng có loại cảm ứng từ mạnh với thành phần từ trường \(\overrightarrow B \) của sóng điện từ như anten ferit.
Để truyền được các thông tin như âm thanh, hình ảnh… đến những nơi xa, người ta đều áp dụng một quy trình là:
+ Biến các âm thanh (hình ảnh…) muốn truyền đi thành các dao động điện gọi là tín hiệu âm tần (thị tần).
+ Dùng sóng điện từ tần số cao (cao tần), gọi là sóng mang, để truyền tín hiệu âm tần đi xa qua anten phát.
+ Dùng máy thu với anten thu để chọn và thu lấy sóng điện từ cao tần.
+ Tách tín hiệu ra khỏi sóng cao tần rồi dùng loa để nghe âm thanh đã truyền tới (hoặc dùng màn hình để xem hình ảnh).
Sơ đồ được thể hiện trong hình 1:
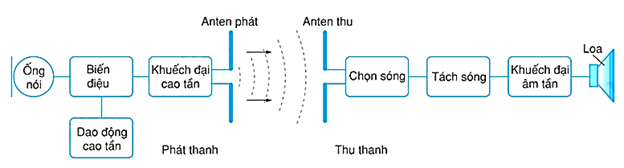
a. Hệ thống phát thanh gồm:
+ Dao động cao tần tạo ra sóng mang.
+ Ống nói (micro): biến âm thanh thành dao động âm tần.
+ Mạch biến điệu: trộn dao động âm tần và dao động cao tần thành dao động cao tần biến điệu
+ Mạch khuếch đại cao tần: khuếch đại dao động cao tần biến điệu để đưa ra anten phát.
+ Anten phát: phát xạ sóng cao tần biến điệu ra không gian
b. Hệ thống thu thanh gồm:
+ Anten thu: cảm ứng với nhiều sóng điện từ.
+ Chọn sóng: chọn lọc sóng muốn thu nhờ mạch cộng hưởng.
+ Tách sóng: lấy ra dao động âm tần từ cao động cao tần biến điệu.
+ Mạch khuếch đại âm tần: là mạnh dao động âm tầm rồi đưa ra loa
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 49
A. Dao động tự do với tần số bằng tần số riêng của mạch
B. Dao động cưỡng bức có tần số bằng tần số riêng của mạch
C. Dao động tắt dần có tần số bằng tần số riêng của mạch
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 50
A. Không thể có một thiết bị vừa thu vừa phát sóng điện từ
B. Để thu sóng điện từ cần dùng một ăng ten
C. Nhờ có ăng ten mà ta có thể chọn lọc được sóng cần thu
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
A. Chỉ có máy phát sóng vô tuyến
B. Chỉ có máy thu sóng vô tuyến
C. Có cả máy phát và thu sóng vô tuyến
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. Độ lớn cực đại và hướng về phía Tây
B. Độ lớn cực đại và hướng về phía Đông
C. Độ lớn bằng không
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
A. 15,5 m đến 41,5 m
B. 13,3 m đến 66,6 m
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 8
Đọc thông tin sau đây và trả lời các câu hỏi từ câu 55- câu 60:
PHẢN ỨNG HẠT NHÂN
Phóng xạ là hiện tượng hạt nhân nguyên tử không bền vững bị biến đổi thành hạt nhân của nguyên tử khác, đồng thời phát ra bức xạ dạng hạt hoặc photon có năng lượng lớn, gọi là tia phóng xạ.
Trong tự nhiên, các nguyên tố phóng xạ tự nhiên có thể phân bố trong đất, nước và trong không khí, được chia thành 4 họ phóng xạ: họ uranium, họ actinium, họ thorium và họ neptinum. Uranium được tìm thấy trong tự nhiên gồm hai đồng vị phổ biến 235U (0,711%) và 238U (99,284%). Uranium có trong đất đá, cũng xuất hiện trong thực vật và trong các mô ở người; cùng họ uranium còn có 226Ra và các sản phẩm phân ra của nó 222Rn, 210Pb, 210Bi,… Thorium chỉ có đồng vị 232Th xuất hiện trong tự nhiên, các đồng vị còn lại đều không bền.
Tia phóng xạ gồm có hạt alpha (α), hạt beta (β) và bức xạ điện từ gamma (γ), được gọi tương ứng là phóng xạ α, phóng xạ β, phóng xạ γ.
- Nhiều phản ứng phân rã hạt nhân tạo ra hạt nhân mới ở trạng thái kích thích có mức năng lượng cao, khi trở về trạng thái cơ bản (bền vững) sẽ phát bức xạ dưới dạng photon có năng lượng cao, gọi là phóng xạ γ. Phóng xạ γ thường đi kèm với phóng xạ α, β.
Các tia α, β, γ có khả năng đâm xuyên và khả năng gây ion hóa khác nhau. Tia α không đâm xuyên được qua giấy, tia β có thể đi xuyên qua giấy, tia γ đi xuyên qua giấy, da, nhựa, nhôm, vonfram,… tuy nhiên khả năng gây ion hóa của tia α là mạnh nhất, tia γ là yếu nhất.
Trong phản ứng hạt nhân, cả số khối và điện tích đều được bảo toàn:
- Phóng xạ α: Sau phóng xạ α, điện tích hạt nhân nguyên tử giảm 2 đơn vị và số khối giảm hẳn 4 đơn vị.
- Phóng xạ β: Sau phóng xạ β, điện tích hạt nhân nguyên tử tăng 1 đơn vị, số khối không thay đổi.
- Phóng xạ β+: Sau phóng xạ β+, điện tích hạt nhân nguyên tử giảm 1 đơn vị, số khối không thay đổi.
- Phóng xạ γ: Không làm thay đổi điện tích hạt nhân nguyên tử và số khối của nguyên tử.
Phản ứng hạt nhân là sự biến đổi hạt nhân nguyên tử của một nguyên tố hóa học này thành hạt nhân nguyên tử của một nguyên tố hóa học khác. Có thể chia thành phản ứng phân hạch và phản ứng nhiệt hạch.
- Phản ứng phân hạch: Dưới tác dụng của neutron, hạt nhân nguyên tử phân chia thành 2 hạt nhân mới, gọi là 2 mảnh phân hạch, đồng thời giải phóng năng lượng. Nhiên liệu chủ yếu của phản ứng phân hạch là 235U và 239Pu.
- Phản ứng nhiệt hạch (Phản ứng tổng hợp hạt nhân): Là quá trình 2 hạt nhân hợp lại để tạo thành hạt nhân mới nặng hơn, đồng thời giải phóng năng lượng. Nhiên liệu thường dùng cho phản ứng nhiệt hạch là đồng vị deuterium và tritium của H.
\(_1^2{\rm{D}} + _1^3{\rm{T}} \to _2^4{\rm{He}} + _0^1n + 17,6\) MeV
Câu 55
A. Đúng
B. Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
A. \(_Z^AX \to _2^4{\rm{He}} + _{Z - 2}^{A - 4}X'\).
B. \(_Z^AX \to _{ - 1}^0e + _{Z + 1}^AX'\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
A. \(_2^4{\rm{He}},\,\,_{ - 1}^0e,\,\,_{ + 1}^0e\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
A. \(_{56}^{141}{\rm{Ba}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 66
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
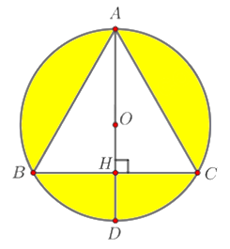
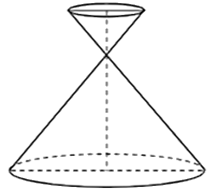
A. \(\frac{{\pi \sqrt 3 {a^3}}}{{24}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
A. \(\frac{{57}}{{286}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
A. \(a\) chia hết cho \(b\).
B. \(a\) và \(b\) nguyên tố cùng nhau.
C. \(a\) và \(b\) nguyên tố cùng nhau.
D. Một trong hai số là số chính phương.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
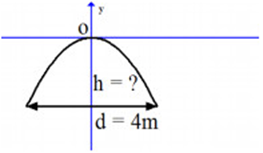
A. \(h = 8m\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.