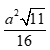100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P4)
16 người thi tuần này 5.0 21.1 K lượt thi 25 câu hỏi 20 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. ba đường thẳng MQ, RA, NP đôi một song song
B. ba đường thẳng MP, NQ, RA đồng quy
C. ba đường thẳng NQ, SP, RS đồng phẳng
D. cả 3 mệnh đề trên đều sai.
Lời giải
Đáp án D
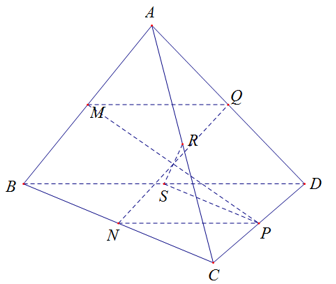
Các phương án đã cho đều sai: Cần sửa thành:
A. MQ, BD, NP đôi một song song
B. Ba đường thẳng MP; NQ; RS đồng quy
C. NQ; SP; RS không đồng phẳng.
Câu 2
A. p và q cắt nhau
B. p và q chéo nhau
C. p và q song song
D. cả 3 mệnh đề trên đều sai
Lời giải
Đáp án D
2 đường thẳng p và q có thể song song, chéo nhau, hoặc cắt nhau
Lời giải
Đáp án D
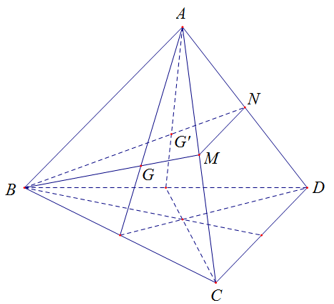
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
(BGG’)(ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = CD = ( MN là đường trung bình của tam giác ACD)
BM = BN = (BM, BN lần lượt là đường trung tuyến - đường cao của tam giác đều ABC, ABD có độ dài cạnh bằng a)
Áp dụng công thức hê- rông :
Trong đó: là nửa chu vi của tam giác
Câu 4
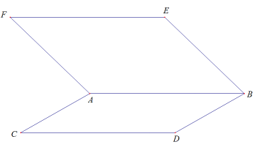
A. AD // (BEF)
B. EC //(ABF)
C. (ABD)//(EFC)
D. Không có đáp án đúng
Lời giải
Đáp án D
Câu 5
A. đường thẳng A’B’
B. đường thẳng A’B’
C. đường thẳng A’C’
D. đường thẳng A’B’
Lời giải
Đáp án C
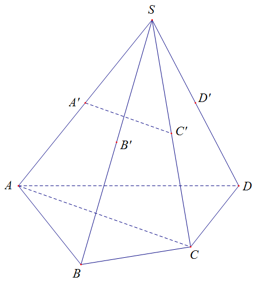
Mặt phẳng (P) đi qua A’ và song song AC
Trong mặt phẳng (SAC), ta có A’C’//AC (A’C’ là đường trung bình tam giác SAC)
(P) đi qua A’C’ cố định
Câu 6
A. MN // (SCD)
B. EF //(SAD)
C. NF // (SAD)
D. IJ //(SAB)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Nếu đường thẳng a(Q) thì a // (P)
B. Mọi đường thẳng đi qua điểm A(P) và song song với (Q) đều nằm trong (P).
C. d(P) và d'(Q) thì d //d'.
D. Nếu đường thẳng cắt (P) thì D cũng cắt (Q).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. Đồng quy
B. Tạo thành tam giác
C. Trùng nhau
D. Cùng song song với một mặt phẳng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau
B. Hai đường thẳng phân biệt không cắt nhau thì chéo nhau
C. Hai đường thẳng phân biệt không song song thì chéo nhau
D. Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Hai mp phân biệt cùng song song với một đường thẳng thì song song với nhau.
B. Hai mp phân biệt cùng song song với một mặt phẳng thì song song với nhau.
C. Nếu một đường thẳng song song với một trong hai mặt phẳng song song thì nó song song với mặt phẳng còn lại.
D. Nếu một đường thẳng nằm trên một trong hai mặt phẳng song song thì nó song song với mọi đường thẳng nằm trong mặt phẳng còn lại.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. Nếu Ad thì A(P).
B. Nếu A(P) thì Ad.
C. A, AdA(P).
D. Nếu 3 điểm A, B, C(P) và A, B, C thẳng hàng thì A, B, Cd
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. BM cắt CD
B. BM song song CD
C. BM cắt AC
D. BM và CD chéo nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. AB
B. BC
C. AC
D.CD
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. a //b và
B. a // mp (Q) và (Q) // (P)
C. a //b và b // (P)
D. và (Q) // (P)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. 1
B. 2
C. 3
D. 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. Có duy nhất một mặt phẳng song song với a và b
B. Có duy nhất một mặt phẳng chứa a và song song với b
C. Có vô số đường thẳng song song với a và cắt b
D. Có duy nhất một mặt phẳng chứa b và song song với a
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. và
B. và
C. a và b cùng chéo với đường thẳng c
D. và
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. Chéo nhau.
B. Song song.
C. Cắt nhau.
D. Có thể song song.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. Có một và chỉ một mặt phẳng đi qua ba điểm đó
B. Có ba và chỉ ba mặt phẳng đi qua ba điểm đó
C. Có vô số mặt phẳng đi qua 3 điểm
D. Không có mặt phẳng nào đi qua 3 điểm đó
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A. Hình bình hành
B. Hình chữ nhật
C. Hình vuông
D. Hình thoi
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.