Đề thi thử Toán Tốt nghiệp TH,THSC&THPT Lê Thánh Tông TP HCM có đáp án

Chọn B

Ta có công thức nguyên hàm của hàm số mũ: \(\int {{a^x}} dx = \frac{{{a^x}}}{{\ln a}} + C\) (với \(a > 0\) và \(a \ne 1\)).

Áp dụng công thức này cho hàm số \(f(x) = {2025^x}\), ta được: \(\int 2 {025^x}dx = \frac{{{{2025}^x}}}{{\ln (2025)}} + C\).

Vậy nguyên hàm của hàm số \(f(x) = {2025^x}\) là \(\frac{{{{2025}^x}}}{{\ln (2025)}} + C\).

Chọn D

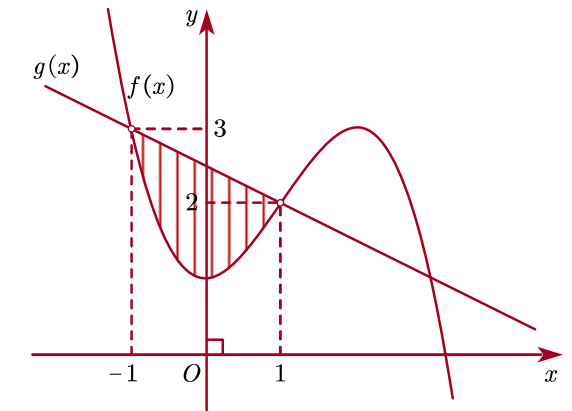
Hoành độ giao điểm là nghiệm của phương trình \(f(x) = g(x)\):

\( - \frac{1}{2}{x^3} + \frac{3}{2}{x^2} + 1 =  - \frac{1}{2}x + \frac{5}{2}\)\( \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 1\\x = 3\end{array} \right.\).

\(S = \int_{ - 1}^1 {\left( {g(x) - f(x)} \right)dx = \int\limits_{ - 1}^1 {\left( {\frac{1}{2}{x^3} - \frac{3}{2}{x^2} - \frac{1}{2}x + \frac{3}{2}} \right)} } dx = 2\).

Chọn B

Tổng số bóng đèn: \(N = 11 + 20 + 29 + 40 + 30 = 130\).

Tần số tích lũy:

 Khoảng [3; 5): 11

 Khoảng [5; 7): \(11 + 20 = 31\)

 Khoảng [7; 9): \(31 + 29 = 60\)

 Khoảng [9; 11): \(60 + 40 = 100\)

 Khoảng [11; 13): \(100 + 30 = 130\)

Để tìm tứ phân vị thứ nhất (\({Q_1}\)), ta xác định vị trí của nó. Vị trí của \({Q_1}\) là \(\frac{N}{4} = \frac{{130}}{4} = 32.5\).

Ta thấy giá trị 32.5 nằm trong khoảng [7; 9). Vậy, nhóm chứa \({Q_1}\) là [7; 9).

\({Q_1} = 7 + \frac{{32.5 - 31}}{{29}} \times 2 = \frac{{206}}{{29}}\).

Chọn B

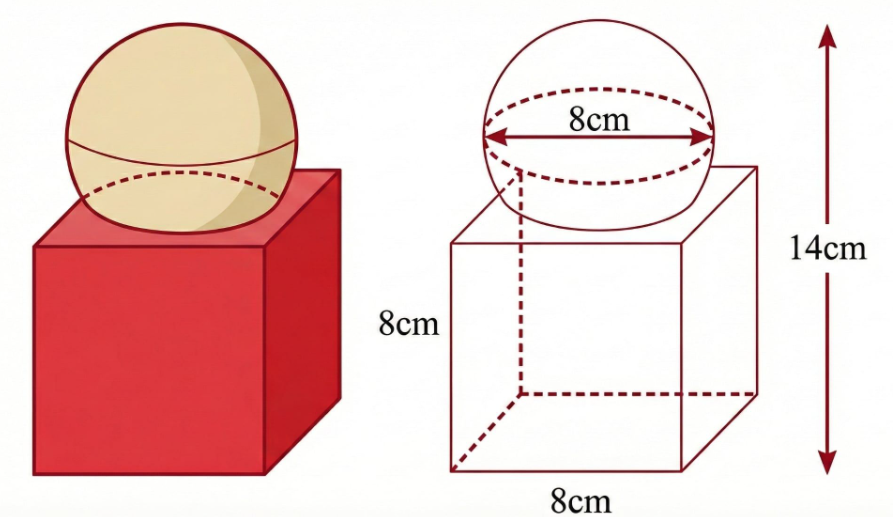
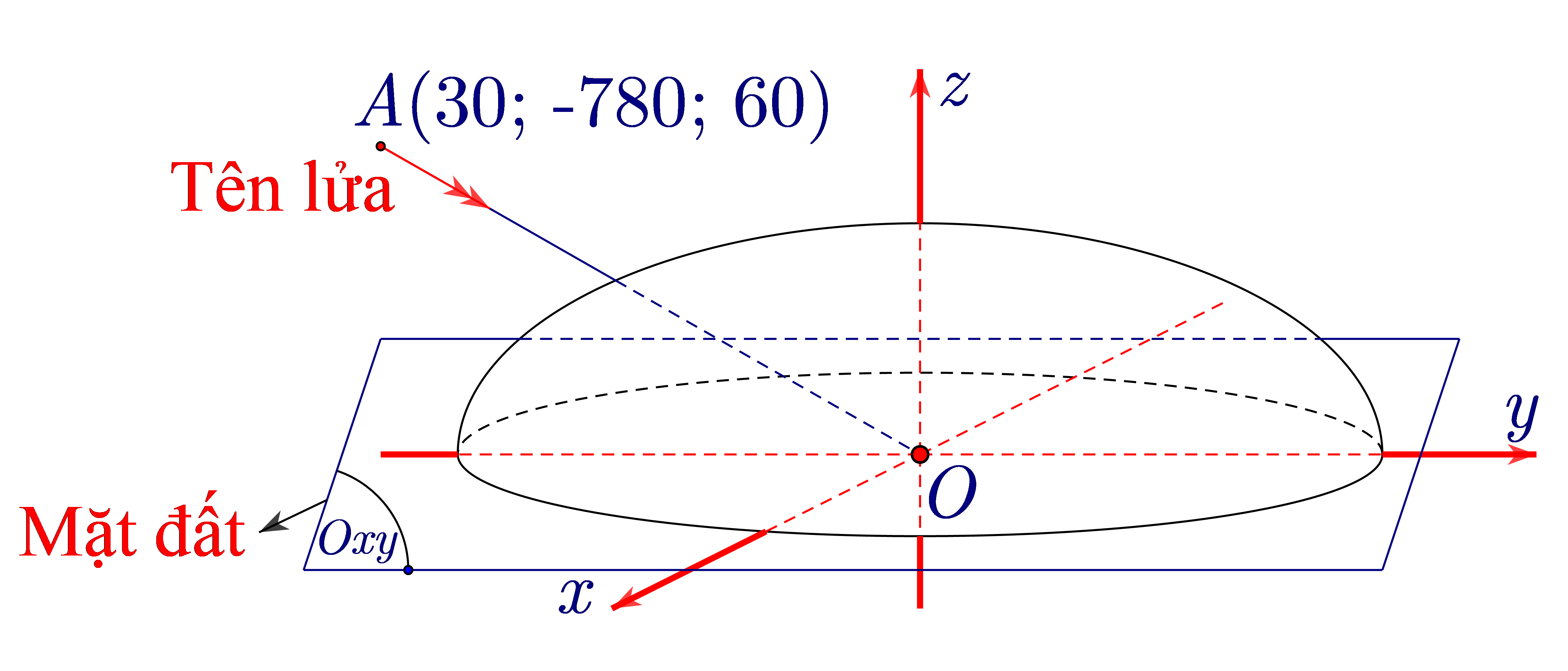
Mặt cầu \((S)\) có tâm \(I(2; - 1;0)\).

Đường kính của mặt cầu là \(d = 8\).

Bán kính của mặt cầu là \(R = \frac{d}{2} = \frac{8}{2} = 4\).

Phương trình tổng quát của mặt cầu có tâm \((a;b;c)\) và bán kính \(R\) là:

\({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\)

Thay tọa độ tâm \(I(2; - 1;0)\) và bán kính \(R = 4\) vào công thức, ta được:

\({(x - 2)^2} + {(y - ( - 1))^2} + {(z - 0)^2} = {4^2}\)\( \Leftrightarrow {(x - 2)^2} + {(y + 1)^2} + {z^2} = 16\).

Chọn A

Xét hàm số \(y = \frac{{ - {x^2} - 2x + 5}}{{x + 2}}\)

Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}.\)

Ta có \(y = \frac{{ - {x^2} - 2x + 5}}{{x + 2}} =  - x + \frac{5}{{x + 2}}.\)

Vì \(\mathop {\lim }\limits_{x \to  + \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to  + \infty } \left( {\frac{{ - {x^2} - 2x + 5}}{{x + 2}} + x} \right) = \mathop {\lim }\limits_{x \to  + \infty } \left( { - x + \frac{5}{{x + 2}} + x} \right) = 0\)

và \(\mathop {\lim }\limits_{x \to  - \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to  - \infty } \left( {\frac{{ - {x^2} - 2x + 5}}{{x + 2}} + x} \right) = \mathop {\lim }\limits_{x \to  - \infty } \left( { - x + \frac{5}{{x + 2}} + x} \right) = 0\)

nên đường thẳng \(y =  - x\)là tiệm cận xiên của đồ thị hàm số đã cho.