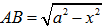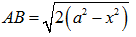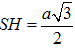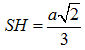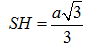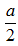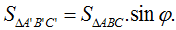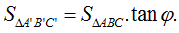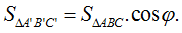16 câu Dạng 3: Tính độ dài đoạn thẳng, diện tích hình chiếu, chu vi và diện tích đa giác có đáp án
28 người thi tuần này 4.6 4.5 K lượt thi 16 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Chọn A
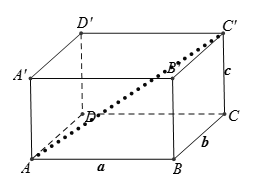
Từ sách giáo khoa, đường chéo hình hộp chữ nhật
Câu 2
Lời giải
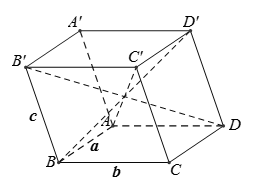
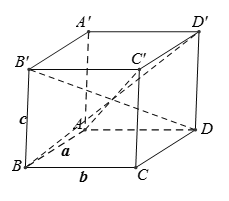
AC' = BD' => hình bình hành ABC'D' là hình chữ nhật
BD' = B'D => hình bình hành BDD'B' là hình chữ nhật
AC' = B'D => hình bình hành ADC'B' là hình chữ nhật
Lời giải
Chọn D
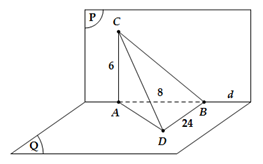
Ta có
Tam giác BCD vuông tại B nên
Câu 4
Lời giải
Chọn C.
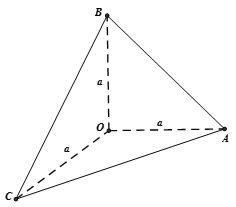
+ Áp dụng định lý Pytago trong tam giác OAB vuông tại O ta có:
Hoàn toàn tương tự ta tính được
là tam giác đều. Mặt khác theo giả thiết OA = OB = OC = a => các mặt bên của hình chóp O.ABC là các tam giác cân tại O => O.ABC là hình chóp đều => đáp án A đúng.
+ Chu vi là: đáp án C sai.
+ Nửa chu vi Diện tích là: . Diện tích là:
(đvdt).
=> đáp án B đúng.
+ Dễ chứng minh được
=> đáp án D đúng.
Câu 5
C.
Lời giải
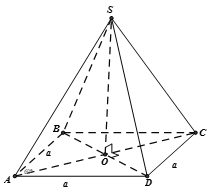
Xét có là tam giác đều cạnh a.
Vì O là tâm của ABCD nên suy ra AO là đường trung tuyến trong đều cạnh a nên dễ tính được .
Mặt khác theo giả thiết SAC là tam giác đều
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.