Ôn thi Tốt nghiệp THPT môn Toán (Đề 13)

421 người thi tuần này 4.6 1.5 K lượt thi 49 câu hỏi 90 phút

Câu 1

Trong không gian, cho tam giác ABC đều cạnh 2a. Gọi M là trung điểm của BC. Khi quay tam giác ABC xung quanh trục AM thì đường gấp khúc ABC tạo thành một hình nón. Tính diện tích xung quanh của hình nón đó

A. $S_{x q} = 2 π a^{2}$

B. $S_{x q} = 4 π a^{2}$

C. $S_{x q} = 6 π a^{2}$

D. $S_{x q} = 8 π a^{2}$

Lời giải

Đáp án đúng là: A

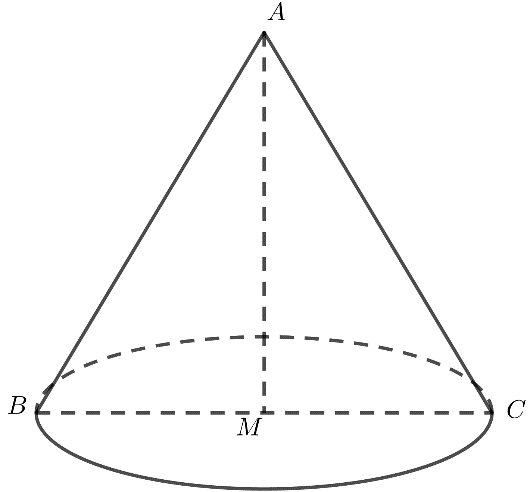
Trong không gian, cho tam giác ABC đều cạnh 2a. Gọi M là trung điểm của BC. Khi quay tam giác ABC xung quanh trục AM thì (ảnh 1)

Ta có hình nón có bán kính đường tròn đáy $r = B M = a$ , đường sinh $l = A B = 2 a$ .

Do đó diện tích xung quanh của hình nón là . $S_{x q} = π r l = 2 π a^{2}$

Câu 2

Thể tích của khối chóp có đáy là tam giác đều cạnh a và chiều cao 4a bằng

A. $a^{3} \sqrt{3}$

B. $4 a^{3}$

C. $\frac{a^{3} \sqrt{3}}{3}$

D. $\frac{4}{3} a^{3}$

Lời giải

Đáp án đúng là: C

Ta có: $V = \frac{1}{3} B h = \frac{1}{3} \frac{a^{2} \sqrt{3}}{4} 4 a = \frac{a^{3} \sqrt{3}}{3}$

Câu 3

Họ các nguyên hàm của hàm số $f (x) = e^{2 x + 3}$ là

A. $\int f (x) d x = \frac{1}{3} e^{2 x + 3} + C$

B. $\int f (x) d x = \frac{1}{2} e^{2 x + 3} + C$

C. $\int f (x) d x = e^{2 x + 3} + C$

D. $\int f (x) d x = 2 e^{2 x + 3} + C$

Lời giải

Đáp án đúng là: B

Áp dụng công thức nguyên hàm mở rộng $\int e^{a x + b} d x = \frac{1}{a} e^{a x + b} + C$ , ta có: $\int e^{2 x + 3} d x = \frac{1}{2} e^{2 x + 3} + C$

Câu 4

Tập xác định của hàm số $y = {(x + 2)}^{\frac{3}{4}}$ là

A. $(- 2; + \infty)$

B. $[- 2; + \infty)$

C. $ℝ$

D. $(0; + \infty)$

Lời giải

Đáp án đúng là: A

Điều kiện $x + 2 > 0 \Leftrightarrow x > - 2$ .

Vậy tập xác định của hàm số là $D = (- 2; + \infty)$

Câu 5

Trong không gian Oxyz, vectơ $\vec{n} = (1; - 1; - 3)$ là một vectơ pháp tuyến của mặt phẳng nào sau đây?

A. $x + y - 3 z - 3 = 0$

B. $x - y + 3 z - 3 = 0$

C. $x - y - 3 z - 3 = 0$

D. $x - 3 z - 3 = 0$

Lời giải

Đáp án đúng là: C

Mặt phẳng $(P) : x - y - 3 z - 3 = 0$ có một vectơ pháp tuyến là: $\vec{n} = (1; - 1; - 3)$ .

Câu 6

Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?

A. $y = \frac{2 x + 1}{x - 1}$

B. $y = x^{4} - 2 x^{2} - 1$

C. $y = x^{3} - 2 x^{2} - 1$

D. $y = - x^{2} + 2 x - 1$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian Oxyz, cho hai vec tơ $\vec{u} = (1; 1; 0)$ và $\vec{v} = (2; 0; - 1)$ . Tính độ dài $|\vec{u} + 2 \vec{v}|$ .

A. 2

B. $2 \sqrt{2}$

C. $\sqrt{30}$

D. $\sqrt{22}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Cho khối lăng trụ có diện tích đáy B = 5 và chiều cao h = 6. Thể tích của khối lăng trụ đã cho bằng

A. 15

B. 10

C. 180

D. 30

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Tập nghiệm của bất phương trình $\log_{3} x < 2$ là

A. $(0; 9)$

B. $(0; + \infty)$

C. $(9; + \infty)$

D. $(- \infty; 9)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Nếu $\int_{0}^{1} f (x) d x = 3$ và $\int_{0}^{3} f (x) d x = - 2$ thì $\int_{1}^{3} f (x) d x$ bằng

A. -6

B. -5

C. 5

D. 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Với n là số nguyên dương bất kỳ, $n \geq 3$ , công thức nào sau đây đúng?

A. $A_{n}^{3} = \frac{n!}{3! (n - 3)!}$

B. $A_{n}^{3} = \frac{n!}{(n - 3)!}$

C. $A_{n}^{3} = \frac{(n - 3)!}{n!}$

D. $A_{n}^{3} = \frac{3! (n - 3)!}{n!}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Phương trình $\log (4 x + 1) = \log (2 x + 5)$ có nghiệm là

A. x = 2

B. x = 1

C. x = 3

D. x = -1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Diện tích S của mặt cầu bán kính r được tính theo công thức nào dưới đây?

A. $S = π r^{2}$

B. $S = 4 π r^{2}$

C. $S = 2 π r^{2}$

D. $S = \frac{4}{3} π r^{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Diện tích S của mặt cầu bán kính r được tính theo công thức nào dưới đây?

A. $S = π r^{2}$

B. $S = 4 π r^{2}$

C. $S = 2 π r^{2}$

D. $S = \frac{4}{3} π r^{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Trong không gian Oxyz cho mặt cầu (S) có phương trình $x^{2} + y^{2} + z^{2} - 2 x + 4 y + 2 z - 4 = 0$ và đi qua điểm M (1;1;0). Mặt phẳng nào dưới đây tiếp xúc với mặt cầu (S) tại M?

A. $3 y + z - 3 = 0$

B. $2 x + 3 y + z - 5 = 0$

C. $3 y + z - 2 = 0$

D. $2 x + 3 y + z + 5 = 0$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Cho cấp số cộng $(u_{n})$ có số hạng đầu $u_{1} = 2$ và công sai $d = 5.$ Giá trị của $u_{4}$ bằng

A. 17

B. 250

C. 12

D. 22

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Nếu $\int_{0}^{1} [f (x) + 2 x] d x = 2$ thì $\int_{0}^{1} f (x) d x$ bằng

A. 4

B. 2

C. 0

D. 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Phần ảo của số phức z = 3 – 4i bằng

A. -4

B. 4

C. 3

D. -4i

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Đường thẳng x = 2 là đường tiệm cận đứng của đồ thị hàm số nào sau đây?

A. $y = \frac{x}{x - 2}$

B. $y = \frac{2 x + 1}{x + 1}$

C. $y = \frac{x - 2}{x + 2}$

D. $y = \frac{- 2 x + 3}{- x + 1} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Chọn ngẫu nhiên hai số khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn là

A. $\frac{313}{625}$

B. $\frac{12}{25}$

C. $\frac{13}{25}$

D. $\frac{1}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Trên đoạn [0;2] hàm số $f (x) = x^{4} - 2 x^{2} + 1$ đạt giá trị lớn nhất tại điểm nào sau đây?

A. x = 0

B. x = 9

C. x = 2

D. x =

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Với mọi số thực a dương, $\log_{2} \frac{a^{2}}{4}$ bằng

A. $\log_{2} a - 2$

B. $2 (\log_{2} a - 1)$

C. $\log_{2} a - 1$

D. $2 \log_{2} a - 1$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 2a. Khoảng cách từ điểm B đến mặt phẳng (ACC’A’) bằng

A. $\sqrt{2} a$

B. $\sqrt{3} a$

C. $2 \sqrt{2} a$

D. 2a

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Cho $\log_{2} 3 = a$ . Tính $P = \log_{8} 6$ theo a.

A. P = 3(1 + a)

B. $P = \frac{1}{3} (1 + a)$

C. $P = 1 + a$

D. $P = 2 + a$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Họ tất cả các nguyên hàm của hàm số $f (x) = \sin x - 6 x^{2}$ là:

A. $\cos x - 12 x + C$

B. $- \sin x - 2 x^{3} + C$

C. $- \cos x - 2 x^{3} + C$

D. $\sin x - 12 x + C$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Trong không gian Oxyz, đường thẳng $Δ : \frac{x - 1}{2} = \frac{y + 3}{1} = \frac{z - 2}{- 3}$ đi qua điểm nào dưới đây?

A. Điểm P (1;3;2)

B. Điểm N (1;-3;2)

C. Điểm M (-1;3;2)

D. Điểm Q (1;-3;-2)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Cho số phức z thỏa mãn (1 – 3i)z + 1 + 7i = 0. Tổng phần thực và phần ảo của z là

A. 1

B. 3

C. -3

D. -6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Tính tích phân $I = \int_{1}^{2} 2 x \sqrt{x^{2} - 1} d x$ bằng cách đặt $u = x^{2} - 1$ mệnh đề nào dưới đây đúng?

A. $I = \frac{1}{2} \int_{1}^{2} \sqrt{u} d u$

B. $I = \int_{1}^{2} \sqrt{u} d u$

C. $I = 2 \int_{0}^{3} \sqrt{u} d u$

D. $I = \int_{0}^{3} \sqrt{u} d u$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Cho hai số phức $z_{1} = 2 - 3 i$ , $z_{2} = 4 + i$ . Số phức $z = z_{1} - z_{2}$ bằng

A. -2 - 4i

B. 2 - 4i

C. 6 + 2i

D. 2 - 2i

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Đồ thị hàm số $y = x^{3} + x^{2} - 2 x - 2$ cắt trục tung tại điểm nào sau đây?

A. M (0;-1)

B. P (-2;0)

C. Q (0;-2)

D. N (-1;0)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Trong không gian Oxyz cho mặt cầu $(S) : {(x + 2)}^{2} + {(y - 6)}^{2} + z^{2} = 4$ . Tâm mặt cầu (S) có tọa độ là

A. (-1;3;0)

B. (2;-6;0)

C. (-2;6;0)

D. (1;-3;0)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Hàm số nào sau đây đồng biến trên $ℝ$ ?

A. $y = - x^{3} + x + 1$

B. $y = \frac{x - 3}{x + 2}$

C. $y = x^{3} + x + 1$

D. $y = x^{4} + x^{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

Đạo hàm của hàm số $y = \ln (x^{2} - 2 x + 1)$ bằng

A. $y^{'} = \frac{1}{x - 1}$

B. $y^{'} = \frac{1}{x^{2} - 2 x + 1}$

C. $y^{'} = \frac{2}{x - 1}$

D. $y^{'} = 2 x - 2$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

Cho hàm số f(x) có bảng biến thiên như sau:

Giá trị cực tiểu $y_{C T}$ của hàm số đã cho là

A. $y_{C T} = - 1$

B. $y_{C T} = 0$

C. $y_{C T} = - 2$

D. $y_{C T} = - 3$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA vuông góc với đáy và $S A = a \sqrt{6}$ . Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng

A. $45 °$

B. $30 °$

C. $60 °$

D. $90 °$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Trong không gian Oxyz, cho điểm A (4;-3;2). Hình chiếu vuông góc của A lên các trục Ox, Oy, Oz theo thứ tự là M; N; P. Phương trình mặt phẳng (MNP) là

A. $\frac{x}{4} - \frac{y}{3} + \frac{z}{2} + 1 = 0$

B. $4 x - 3 y + 2 z - 5 = 0$

C. $3 x - 4 y + 6 z - 12 = 0$

D. $2 x - 3 y + 4 z - 1 = 0$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Cho hàm số $y = a x^{4} + b x^{2} + c (a, b, c \in ℝ)$ có đồ thị là đường cong như hình vẽ.

Giá trị cực tiểu của hàm số đã cho là

A. 1

B. 0

C. 2

D. -1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

Cho hai số phức $z_{1}, z_{2}$ thỏa mãn $|z - 3 - 2 i| = |\bar{z} - 1|, |z_{1} - z_{2}| = 2 \sqrt{2}$ và số phức w thoả mãn $|w - 2 - 4 i| = 1$ . Giá trị nhỏ nhất của biểu thức $P = |z_{2} - 2 - 3 i| + |z_{1} - w|$ bằng

A. $\sqrt{26}$

B. $\sqrt{10}$

C. $\sqrt{17} - 1$

D. 4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

Có bao nhiêu số nguyên x thỏa mãn $(2^{x^{2}} - 4^{x}) [\log_{3} (x + 25) - 3] \leq 0$ ?

A. 25

B. Vô số

C. 26

D. 24

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

Tìm số giá trị nguyên của tham số thực m để tồn tại các số thực x;y thỏa mãn $e^{x^{2} + y^{2} - m} + e^{x + y + x y - m} = x^{2} + y^{2} + x + y + x y - 2 m + 2$ .

A. 7

B. 9

C. 8

D. 6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Trong không gian với hệ toạ độ Oxyz, cho hai mặt phẳng (P): x – y + z + 3 = 0, (Q): x + 2y – 2z – 5 = 0 và mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 y - 6 z - 11 = 0$ . Gọi M là điểm di động trên (S) và N là điểm di động trên (P) sao cho MN luôn vuông góc với (Q). Giá trị lớn nhất của độ dài đoạn thẳng MN bằng

A. $9 + 5 \sqrt{3}$

B. 14

C. 28

D. $3 + 5 \sqrt{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Trong không gian với hệ tọa độ Oxyz, từ điểm A (1;1;0) ta kẻ các tiếp tuyến đến mặt cầu (S) có tâm I (-1;1;1), bán kính R =1. Gọi M (a;b;c) là một trong các tiếp điểm ứng với các tiếp tuyến trên. Tìm giá trị lớn nhất của biểu thức $T = |2 a - b + 2 c|$

A. $\frac{3 + \sqrt{41}}{15} .$

B. $\frac{3 + \sqrt{41}}{5} .$

C. $\frac{3 + 2 \sqrt{41}}{15} .$

D. $\frac{3 + 2 \sqrt{41}}{5} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

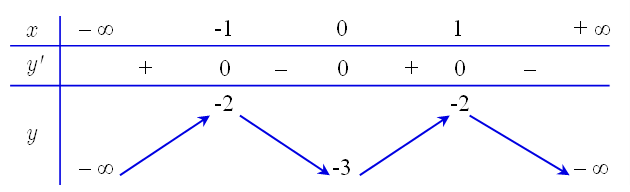
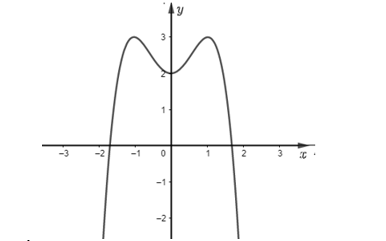
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số m để phương trình $f [f (|x + 1|) - 2] = m$ có 10 nghiệm phân biệt thuộc đoạn [-3;3]?

A. 3

B. 1

C. 0

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

Cho hình lăng trụ ABC.A’B’C’có đáy ABC là tam giác vuông tại A, BC = 2a và góc $\hat{A B C} = 60 °$ . Biết tứ giác BCC’B’ là hình thoi có $\hat{B^{'} B C}$ nhọn, mặt phẳng (BCC’B’) vuông góc mặt phẳng (ABC), góc giữa hai mặt phẳng (ABB’A’) và (ABC) bằng $45 °$ . Thể tích khối lăng trụ bằng

A. $\frac{a^{3}}{\sqrt{7}}$

B. $\frac{a^{3}}{3 \sqrt{7}}$

C. $\frac{3 a^{3}}{\sqrt{7}}$

D. $\frac{6 a^{3}}{\sqrt{7}}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

Cho hàm số bậc ba y = f(x) có đồ thị là đường cong ở hình bên dưới.

Gọi $x_{1}, x_{2}$ lần lượt là hai điểm cực trị thỏa mãn $x_{2} = x_{1} + 2$ và $f (x_{1}) - 3 f (x_{2}) = 0$ . và đồ thị luôn đi qua $M (x_{0}; f (x_{0}))$ , trong đó $x_{0} = x_{1} - 1; g (x)$ là hàm số bậc hai có đồ thị qua 2 điểm cực trị của đồ thị hàm số y = f(x) và điểm M. Tính tỉ số $\frac{S_{1}}{S_{2}}$ ( $S_{1}$ và $S_{2}$ lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai hàm $f (x), g (x)$ như hình vẽ).

A. $\frac{4}{29}$

B. $\frac{5}{32}$

C. $\frac{7}{33}$

D. $\frac{6}{35}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên dưới.

Số nghiệm thực của phương trình $|f (x^{4} - 2 x^{2})| = 2$ là

A. 7

B. 9

C. 10

D. 8

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

Trên tập hợp số phức, xét phương trình $z^{2} - 6 z + m = 0 (m$ là tham số thực). Gọi $m_{0}$ là một giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt $z_{1}, z_{2}$ thỏa mãn $z_{1} . \bar{z_{1}} = z_{2} . \bar{z_{2}}$ . Trong khoảng (0;20) có bao nhiêu giá trị nguyên $m_{0}$ ?

A. 13

B. 10

C. 11

D. 12

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

Trong không gian Oxyz, cho hai điểm A (2;1;3), B (6;5;5). Xét khối nón (N) ngoại tiếp mặt cầu đường kính AB có B là tâm đường tròn đáy khối nón. Gọi S là đỉnh của khối nón (N). Khi thể tích khối nón (N) nhỏ nhất thì mặt phẳng qua đỉnh S và song song với mặt phẳng chứa đường tròn đáy của (N) có phương trình 2x + by + cz + d = 0. Tính T = b + c + d.

A. T = 12

B. T = 18

C. T = 24

D. T = 36

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Cho hàm số f(x) có đạo hàm liên tục trên $ℝ$ . Biết f(5) = 1 và $\int_{0}^{1} x f (5 x) d x = 1$ , khi đó $\int_{0}^{5} x^{2} f^{'} (x) d x$ bằng

A. -25

B. 23

C. 15

D. $\frac{123}{5}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử