Dạng 2: Tính góc giữa đường thẳng và mặt phẳng có đáp án

22 người thi tuần này 4.6 3.4 K lượt thi 31 câu hỏi 45 phút

🔥 Đề thi HOT:

1145 người thi tuần này

Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)

31.6 K lượt thi 30 câu hỏi

559 người thi tuần này

Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)

13.4 K lượt thi 30 câu hỏi

361 người thi tuần này

12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án

4.1 K lượt thi 12 câu hỏi

156 người thi tuần này

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 1)

10.2 K lượt thi 39 câu hỏi

141 người thi tuần này

10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)

10.5 K lượt thi 10 câu hỏi

140 người thi tuần này

184 câu Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác có đáp án (Mới nhất)

4.6 K lượt thi 184 câu hỏi

128 người thi tuần này

10 Bài tập Bài toán thực tiễn liên quan đến giá trị lượng giác của góc lượng giác (có lời giải)

1 K lượt thi 10 câu hỏi

111 người thi tuần này

Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)

14.9 K lượt thi 25 câu hỏi

Nội dung liên quan:

10 câu Trắc nghiệm Vectơ trong không gian có đáp án

lượt thi

1 đề

15 câu Trắc nghiệm Vectơ trong không gian có đáp án (Nhận biết)

lượt thi

1 đề

15 câu Trắc nghiệm Vectơ trong không gian có đáp án (Thông hiểu)

lượt thi

1 đề

10 câu Trắc nghiệm Vectơ trong không gian có đáp án (Vận dụng)

lượt thi

1 đề

12 câu Trắc nghiệm Hai đường thẳng vuông góc với nhau có đáp án

lượt thi

1 đề

15 câu Trắc nghiệm Hai đường thẳng vuông góc có đáp án (Nhận biết)

lượt thi

1 đề

15 câu Trắc nghiệm Hai đường thẳng vuông góc có đáp án (Thông hiểu)

lượt thi

1 đề

11 câu Trắc nghiệm Hai đường thẳng vuông góc có đáp án (Vận dụng)

lượt thi

1 đề

81 câu Trắc nghiệm Toán 11 Bài 2: Hai đường thẳng vuông góc có đáp án (Mới nhất)

lượt thi

3 đề

22 câu Trắc nghiệm Đường thẳng vuông góc với mặt phẳng có đáp án

lượt thi

1 đề

Danh sách câu hỏi:

Câu 1

Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?

A. Góc giữa AC và (BCD) là góc ACB

B. Góc giữa AD và (ABC) là góc ADB

C. Góc giữa AC và (ABD) là góc CAB

D. Góc giữa CD và (ABD) là góc CBD

Lời giải

Chọn A.

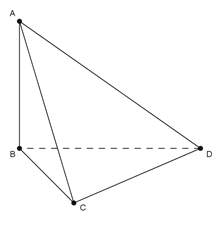
Cho tứ diện ABCD có cạnh AB, BC, BD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng? (ảnh 1)

Từ giả thiết ta có $\{\begin{cases} A B ⊥ B C \\ A B ⊥ C D \end{cases} \Rightarrow A B ⊥ (B C D)$

Do đó $(A C, (B C D)) = \hat{A C B}$

Câu 2

Cho tam giác ABC vuông cân tại A và BC = a. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm S sao cho $S A = \frac{a \sqrt{6}}{2}$ . Tính số đo góc giữa đường thẳng SA và (ABC)

A. 30°

B. 45°

C. 60°

D. 90°

Lời giải

Chọn D.

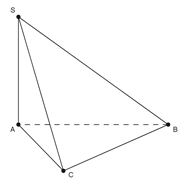
Cho tam giác ABC vuông cân tại A và BC = a. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm S sao cho (ảnh 1)

S A ⊥ (A B C) \Rightarrow (S A, (A B C)) = 90 °

Câu 3

Cho tứ diện ABCD có cạnh AB, BC, BD vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng ?

A. Góc giữa CD và (ABD) là góc

\hat{C B D}

B. Góc giữa AC và (BCD) là góc

\hat{A C B}

C. Góc giữa AD và (ABC) là góc

\hat{A D B}

D. Góc giữa AD và (ABD) là góc

\hat{C B A}

Lời giải

Chọn B

Do AB, BC, BD vuông góc với nhau từng đôi một nên $A B ⊥ (B C D)$ , suy ra BC là hình chiếu của AC lên $(B C D)$

Câu 4

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và (ABC).

A. 30°

B. 45°

C. 60°

D. 75°

Lời giải

Chọn C.

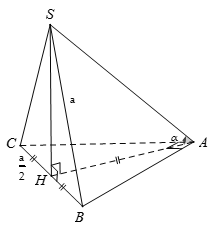
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. (ảnh 1)

Gọi H là trung điểm của BC suy ra $A H = B H = C H = \frac{1}{2} B C = \frac{a}{2}$

Ta có: $S H ⊥ (A B C) \Rightarrow S H = \sqrt{S B^{2} - B H^{2}} = \frac{a \sqrt{3}}{2}$

$\hat{(S A, (A B C))} = \hat{S A H} = α \Rightarrow \tan α = \frac{S H}{A H} = \sqrt{3} \Rightarrow α = 60 °$

Câu 5

Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và $S A ⊥ (A B C D)$ . Biết $S A = \frac{a \sqrt{6}}{3}$ . Tính góc giữa SC và (ABCD)

A. 30°

B. 45°

C. 60°

D. 75°

Lời giải

Chọn A.

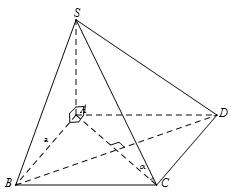
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và SA vuông góc mp ABCD. Biết SA = a căn bậc hai 6/3 . (ảnh 1)

Ta có: $S A ⊥ (A B C D) \Rightarrow S A ⊥ A C$

$\Rightarrow \hat{(S C; (A B C D))} = \hat{S C A} = α$

ABCD là hình vuông cạnh a

\Rightarrow A C = a \sqrt{2}, S A = \frac{a \sqrt{6}}{3} \Rightarrow \tan α = \frac{S A}{A C} = \frac{\sqrt{3}}{3} \Rightarrow α = 30 °

Câu 6

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)

A. 60°

B. 75°

C. 45°

D. 30°

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử