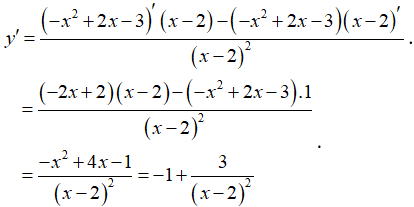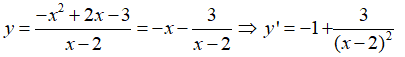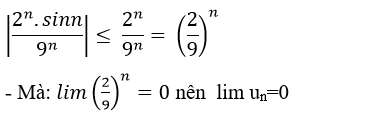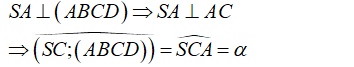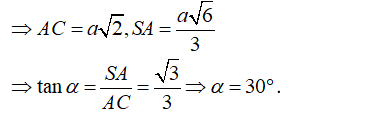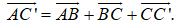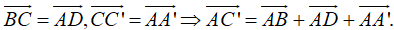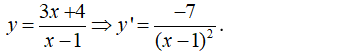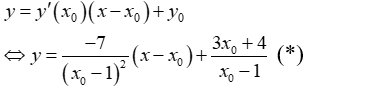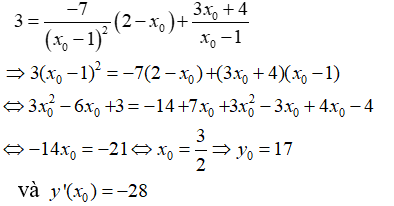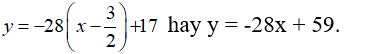Đề thi Học kì 2 Toán 11 có đáp án (Đề 3)
20 người thi tuần này 5.0 11.5 K lượt thi 30 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 6 (có lời giải) - Đề 1
Đề kiểm tra Phương trình – bất phương trình mũ và lôgarit (có lời giải) - Đề 3
Đề kiểm tra Phương trình – bất phương trình mũ và lôgarit (có lời giải) - Đề 2
Đề kiểm tra Phương trình – bất phương trình mũ và lôgarit (có lời giải) - Đề 1
Danh sách câu hỏi:
Lời giải
Đáp án C
Cách 1: Ta có:
Cách 2: Ta có:
Lời giải
Đáp án A
- Theo công thức giới hạn đặc biệt, ta có:
Câu 3
A. 30°
B. 45°
C. 60°
D. 75°
Lời giải
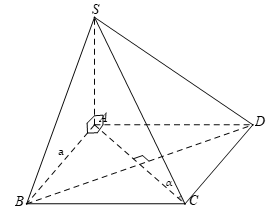
Đáp án A.
- Ta có:
- Vì ABCD là hình vuông cạnh a.
Lời giải
Đáp án C.
- Phương pháp: Sử dụng công thức ba điểm và các vectơ bằng nhau.
- Cách giải:
+ Ta có:
+ Mà:
Câu 5
A. y = -28x+59; y = x+1
B. y = -24x+59; y = x+1
C. y = -28x+59
D. y = -28x+59; y = -24x+51
Lời giải
Đáp án C.
- Ta có:
- Phương trình tiếp tuyến của đồ thị (C): 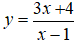
- Vì tiếp tuyến đi qua điểm A(2; 3) nên ta có:
- Vậy có một tiếp tuyến thỏa đề bài là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. a = 10, b = 11
B. a = 0, b = -1
C. a = 0, b = 1
D. a = 20, b = 1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. SA⊥BC
B. AH⊥BC
C. AH⊥AC
D. AH⊥SC
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. Vận tốc của chuyển động bằng 0 khi t = 0 hoặc t = 2.
B. Vận tốc của chuyển động tại thời điểm t= 2 là v = 18m/s.
C. Gia tốc của chuyển động tại thời điểm t = 3 là
D. Gia tốc của chuyển động bằng 0 khi t = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. y = 8x-6; y = -8x-6
B. y = 8x-6; y = -8x+6
C. y = 8x-8; y = -8x+8
D. y = 40x-57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. a = -1, b = 1
B. a = -1, b = 2
C. a = -1, b = 3
D. a = -1, b = 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.