Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P2)

Thi Online Bài tập Hình học không gian cơ bản, nâng cao có lời giải

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P2)

9633 lượt thi
30 câu hỏi
50 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng $a \sqrt{3}$ . Gọi $V_{1}, V_{2}$ lần lượt thể tích khối cầu và khối nón ngoại tiếp hình chóp S.ABCD. Tính tỷ số $\frac{V_{1}}{V_{2}}$

A. $\frac{V_{1}}{V_{2}} = \frac{324}{25}$

B. $\frac{V_{1}}{V_{2}} = \frac{18 \sqrt{30}}{25}$

C. $\frac{V_{1}}{V_{2}} = \frac{36}{25}$

D. $\frac{V_{1}}{V_{2}} = \frac{108}{25}$

Xem đáp án

Đáp án D.

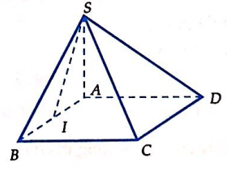
Gọi O là tâm của hình vuông ABCD.vì S.ABCD là hình chop đều nên SO $⊥$ (ABCD)

Từ giả thiết, ta có

Khối nón ngoại tiếp hình chóp S.ABCD có chiều cao

và bán kính đáy là

và bán kính đáy là

Suy ra

Ta có SO là trục đường tròn ngoại tiếp hình vuông ABCD. Đường trung trực của SB nằm trong mặt phẳng (SBD) cắt SB, SO lần lượt tại M, I. Ta có IS = IB = IA = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.

Ta có SI.SO = SM.SB

Suy ra

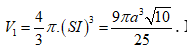
Do đó $\frac{V_{1}}{V_{2}} = \frac{108}{25}$

Phân tích phương án nhiễu.

Phương án A: Sai do HS nhớ nhầm công thức tính thể tích khối cầu là

Do đó tính được $\frac{V_{1}}{V_{2}} = \frac{324}{25}$

Phương án B: Sai do HS nhớ nhầm công thức tính thể tích khối nón là

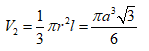
Do đó tính được $\frac{V_{1}}{V_{2}} = \frac{18 \sqrt{30}}{25}$

Phương án C: Sai do HS nhớ sai công thức tính thể tích khối nón là

Do đó tính được $\frac{V_{1}}{V_{2}} = \frac{36}{25}$

Câu 2:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2 $\sqrt{3}$ . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi M, N, P lần lượt là trung điểm của các cạnh SA, CD, CB. Tính côsin góc tạo bởi mặt phẳng (MNP) và (SCD).

A. $\frac{2 \sqrt{435}}{145}$

B. $\frac{11 \sqrt{435}}{145}$

C. $\frac{2 \sqrt{870}}{145}$

D. $\frac{3 \sqrt{145}}{145}$

Xem đáp án

Đáp án B.

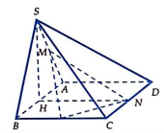
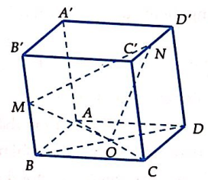
Gọi H là trung điểm của cạnh AB. Khi đó SH $⊥$ (ABCD)

Ta có SH $⊥$ AB; AB $⊥$ HN; HN $⊥$ SH và SH = $\sqrt{3}$

Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó: B(1;0;0), A(-1;0;0), N(0;2 $\sqrt{3}$ ;0), C(1;2 $\sqrt{3}$ ;0)

D(-1;2 $\sqrt{3}$ ;0), S(0;0; $\sqrt{3}$ ), M( $- \frac{1}{2}; 0; \frac{\sqrt{3}}{2}$ ), P(1; $\sqrt{3}$ ;0)

Mặt phẳng (SCD) nhận

làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận

làm một vectơ pháp tuyến.

Gọi $φ$ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì

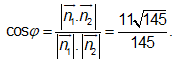
Phân tích phương án nhiễu.

Phương án A: Sai do HS tính đúng

nhưng lại tính sai Do đó tính được

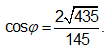
Phương án B: Sai do HS tính đúng nhưng lại tính sai

Do đó tính được

Phương án C: Sai do HS tính đúng nhưng lại tính sai

Do đó tính được

Câu 3:

Một người thợ có một khối đá hình trụ có bán kính đáy bằng 30cm. Kẻ hai đường kính MN, PQ của hai đáy sao cho . Người thợ đó cắt khối đá theo các mặt cắt đi qua ba trong bốn điểm M, N, P,Q để được một khối đá có hình tứ diện (như hình vẽ dưới). Biết rằng khối tứ diện MNPQ có thể tích bằng . Thể tích của lượng đá bị cắt bỏ gần với kết quả nào dưới đây nhất?

A. 111,40 $d m^{3}$

B. 111,39 $d m^{3}$

C. 111,30 $d m^{3}$

D. 111,35 $d m^{3}$

Xem đáp án

Đáp án B.

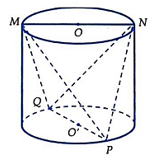
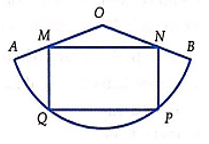
Trước hết ta có kết quả: Khối tứ diện ABCD có thể tích được tính theo công thức

Áp dụng kết quả này, ta có

= 6h

trong đó MN = PQ = 6 dm và h = d(MN;PQ) là chiều cao của hình trụ.

Từ giả thiết ta có h = 5 dm

Suy ra thể tích khối trụ là , với r = 3 dm

Do đó thể tích của lượng đá bị cắt bỏ là

Vậy phương án đúng là B.

Phân tích phương án nhiễu.

Phương án A và C: Sai do HS giải đúng nhưng làm tròn số bị sai hoặc lấy

Phương án D: Sai do HS chọn $π$ = 3,141

Câu 4:

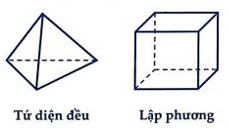
Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ:

Mệnh đề nào sau đây đúng?

A. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.

B. Mọi khối lập phương và khối bát diện đều có cùng số cạnh.

C. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.

D. Khối 12 mặt đều và khối 20 mặt đều có cùng số đỉnh.

Xem đáp án

Đáp án B.

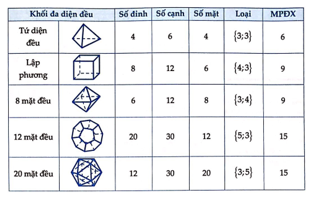
Như vậy, khối lập phương và khối bát diện đều có số cạnh bằng nhau (12 cạnh).

Câu 5:

Cho hai đường thẳng phân biệt a,b và mặt phẳng ( $α$ ). Mệnh đề nào sau đây là đúng?

A. Nếu a//( $α$ ) và b//( $α$ ) thì b//a.

B. Nếu a//( $α$ ) và b $⊥$ $α$ thì b $⊥$ $α$ .

C. Nếu a// $α$ ) và b $⊥$ ( $α$ ) thì a $⊥$ b.

D. Nếu a $⊥$ ( $α$ ) và b $⊥$ a thì .

Xem đáp án

Đáp án D.

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P1)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P3)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P4)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P5)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P6)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P7)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P8)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P9)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P10)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P11)

30 câu hỏi 50 phút

Bài tập Hình học không gian cơ bản, nâng cao có lời giải (P12)

30 câu hỏi 50 phút

Các bài thi hot trong chương:

93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải

( 45.2 K lượt thi )

299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết

( 18 K lượt thi )

160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án

( 12.1 K lượt thi )

Bài tập Tổ Hợp - Xác Suất từ đề thi đại học cực hay có lời giải

( 8.3 K lượt thi )

Bài tập Lượng giác từ đề thi đại hoc cơ bản, nâng cao có đáp án

( 7.8 K lượt thi )

0

Đánh giá trung bình

0%

0%

0%

0%

0%

Bình luận

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack