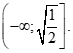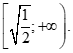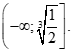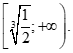167 câu Trắc nghiệm Toán 11 Dạng 3: Đạo hàm và các bài toán giải pt, bpt có đáp án (Mới nhất)
34 người thi tuần này 4.6 5.3 K lượt thi 26 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 7 (có lời giải) - Đề 1
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 3
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 2
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 1
Đề kiểm tra Bài tập cuối chương 6 (có lời giải) - Đề 3
Danh sách câu hỏi:
Câu 1
Lời giải
Hướng dẫn giải:
Chọn B.
Ta có : \(y' = 3{x^2} - 6x - 9\)
\(y' = 0 \Leftrightarrow 3{x^2} - 6x - 9 = 0 \Leftrightarrow x = - 1;x = 3\).
Câu 2
Lời giải
Hướng dẫn giải:
Chọn C.
Ta có: \[f\left( x \right) = k\sqrt[3]{x} + \sqrt x \]\[ \Rightarrow f'\left( x \right) = {\left( {k\sqrt[3]{x} + \sqrt x } \right)^\prime } = k{\left( {\sqrt[3]{x}} \right)^\prime } + {\left( {\sqrt x } \right)^\prime }\]
Đặt \(y = \sqrt[3]{x} \Rightarrow {y^3} = x \Rightarrow 3{y^2}y' = 1 \Rightarrow y' = \frac{1}{{3{y^2}}} = \frac{1}{{3{{\left( {\sqrt[3]{x}} \right)}^2}}}\).
\[f'\left( x \right) = k{\left( {\sqrt[3]{x}} \right)^\prime } + {\left( {\sqrt x } \right)^\prime }\]\[ = \frac{k}{{3{{\left( {\sqrt[3]{x}} \right)}^2}}} + \frac{1}{{2\sqrt x }}\].Vậy để \[f'\left( 1 \right) = \frac{3}{2}\] thì \[\frac{k}{3} + \frac{1}{2} = \frac{3}{2} \Rightarrow k = 3\].
Câu 3
Lời giải
Hướng dẫn giải:
Chọn D
Ta có \(f'(x) = {x^2} - 4\sqrt 2 x + 8\)
\(f'(x) = 0 \Leftrightarrow {x^2} - 4\sqrt 2 x + 8 = 0 \Leftrightarrow x = 2\sqrt 2 \).
Câu 4
Lời giải
Hướng dẫn giải:
Chọn C
\(y' = 4 - \frac{1}{{2\sqrt x }}\)
\(y' = 0 \Leftrightarrow 4 - \frac{1}{{2\sqrt x }} = 0 \Leftrightarrow 8\sqrt x - 1 = 0 \Leftrightarrow \sqrt x = \frac{1}{8} \Rightarrow x = \frac{1}{{64}}\).
Câu 5
Lời giải
Hướng dẫn giải:
Chọn B
Ta có \(y = - 4{x^3} + 4x\)\( \Rightarrow y' = - 12{x^2} + 4\).
Nên \(y' \ge 0 \Leftrightarrow - 12{x^2} + 4 \ge 0 \Leftrightarrow x \in \left[ { - \frac{1}{{\sqrt 3 }};\frac{1}{{\sqrt 3 }}} \right].\)
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.