ĐGNL ĐHQG Hà Nội - Khoa học tự nhiên - Công suất tiêu thụ của mạch điện xoay chiều - Hệ số công suất
49 người thi tuần này 4.6 2.1 K lượt thi 7 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Lời giải
Ta có: \[\left( {{u_d},u} \right) = 1,56rad = \frac{\pi }{2};U = 6V;{U_d} = 10V\]
Vì điện áp hai đầu cuộn dây lệch pha với điện áp hai đầu đoạn mạch góc 1,56rad nên cuộn dây có điện trở thuần.
Ta có giản đồ vecto:
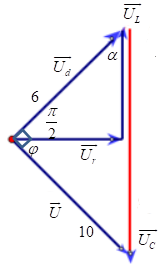
Từ giản đồ vecto ta có: \[\tan \alpha = \frac{6}{{10}} = 0,6\]
\[ \Rightarrow \alpha = shif\tan 0,6 = 0,54042 \Rightarrow cos\alpha = 0,86\]
Mà \[\alpha = \varphi \Rightarrow \cos \varphi = 0,86\]
Đáp án cần chọn là: D
Lời giải
Ta có:
+ Dung kháng:
\[{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}} = \frac{1}{{2\pi .50.\frac{{{{10}^{ - 3}}}}{{8\pi }}}} = 80{\rm{\Omega }}\]
+ Tổng trở của mạch:
\[Z = \sqrt {{R^2} + {Z_C}^2} = \sqrt {{{60}^2} + {{80}^2}} = 100{\rm{\Omega }}\]
+ hệ số công suất:
\[{\rm{cos}}\varphi = \frac{R}{Z} = \frac{{60}}{{100}} = 0,6\]
Đáp án cần chọn là: A
Lời giải
Ta có:
+ Cảm kháng:
\[{Z_L} = \omega L = 2\pi fL = 2\pi .50.\frac{{0,4}}{\pi } = 40{\rm{\Omega }}\]
+ Dung kháng:
\[{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}} = \frac{1}{{2\pi .50.\frac{{{{10}^{ - 4}}}}{\pi }}} = 100{\rm{\Omega }}\]
+ Tổng trở của mạch:
\[Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {{{80}^2} + {{(40 - 100)}^2}} = 100{\rm{\Omega }}\]
+ Cường độ dòng điện hiệu dụng trong mạch:
\[I = \frac{U}{Z} = \frac{{220}}{{100}} = 2,2(A)\]
+ Công suất tỏa nhiệt :
\[P = {I^2}R = {2,2^2}.80 = 387,2{\rm{W}}\]
Đáp án cần chọn là: D
Lời giải
Cường độ dòng điện hiệu dụng trong mạch là:
\[I = \frac{P}{{U\cos \varphi }} = \frac{{1200}}{{220.1}} = \frac{{60}}{{11}} \approx 5,45\left( A \right)\]
Đáp án cần chọn là: C
Câu 5
A.0,42 rad.
B.0,48 rad.
C.0,52 rad.
D.0,32 rad.
Lời giải
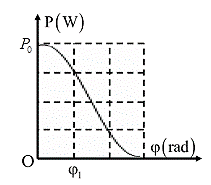
Từ đồ thị ta có:
Khi \[\varphi = 0 \to {P_{ma{\rm{x}}}} = {P_0} = \frac{{{U^2}}}{R}\,\,\,\,\left( 1 \right)\]
Khi \[\varphi = {\varphi _1} \to P = \frac{3}{4}{P_0} = UI\cos \varphi = \frac{{{U^2}}}{{{Z^2}}}R\,\,\,\,\,\left( 2 \right)\]
Từ (1) và (2) ta suy ra: \[\frac{3}{4}\frac{{{U^2}}}{R} = \frac{{{U^2}}}{{{Z^2}}}R\]
\[ \Rightarrow 3{{\rm{Z}}^2} = 4{{\rm{R}}^2} \Leftrightarrow 3\left( {{R^2} + Z_L^2} \right) = 4{{\rm{R}}^2} \Rightarrow {Z_L} = \frac{R}{{\sqrt 3 }}\]
Lại có: \[\tan {\varphi _1} = \frac{{{Z_L}}}{R} = \frac{1}{{\sqrt 3 }} \Rightarrow {\varphi _1} = \frac{\pi }{6}\;rad\]
Đáp án cần chọn là: C
Câu 6
A.2,5W.
B.4,5W.
C.9W.
D.18W.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.\[242\sqrt 2 W\]
B. 242W
C. 121W
D. \(121\sqrt 2 {\rm{W}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.