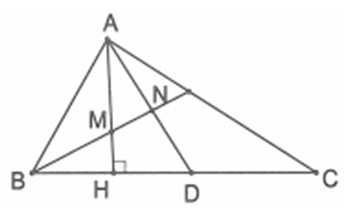
Ta có AMN = BMH = 90 $°$ - MBH, NDH = 90 $°$ - HAD mà MBH = $\frac{1}{2}$ ABC, HAD = $\frac{1}{2}$ HAC và ABC = HAC do cùng phụ với góc BCA, từ đó suy ra AMN = ADH hay tứ giác MHDN nội tiếp => MND = MHD = 90 $°$ .

Câu 2/6

Cho tam giác ABC cân tại A và nội tiếp trong đường tròn tâm O, đường kính AI. Gọi E là trung điểm của AB, K là trung điểm của OI, H là trung điểm của EB.

a) Chứng minh HK $⊥$ AB.

Xem đáp án

Lời giải

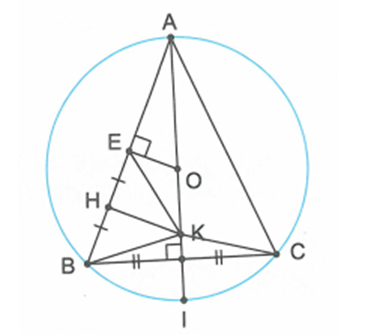
Tam giác ABI nội tiếp đường tròn đường kính AI nên tam giác ABI vuông tại B.

=> IB $⊥$ AB.

Lại có OE $⊥$ AB (quan hệ đường kính và dây cung). Do đó OE // IB. Suy ra OEBI là hình thang.

Mà HK là đường trung bình của hình thang OEBI => HK // OE // IB => HK $⊥$ EB.

Câu 3/6

b) Chứng minh tứ giác AEKC nội tiếp được trong một đường tròn.

Xem đáp án

Lời giải

$∆$ EB cân tại K vì có KH vừa là trung tuyến đồng thời là đường cao => BEK = KBE. (1)

$∆$ ABC cân và có AI là đường kính của đường tròn (O) nên AK là đường trung trực của đoạn BC

=> ABK = ACK. (2)

Từ (1) và (2) suy ra BEK = ACK. Mà BEK là góc ngoài tại đỉnh E của tứ giác AEKC nên tứ giác AEKC nội tiếp.

Câu 4/6

Cho nửa đường tròn tâm I, đường kính MN. Kẻ tiếp tuyến Nx và lấy điểm P chính giữa của nửa đường tròn. Trên cung PN, lấy điểm Q (không trùng với P, N ). Các tia MP và MQ cắt tiếp tuyến Nx theo thứ tự tại S và T.

a) Chứng minh NS = MN.

Xem đáp án

Lời giải

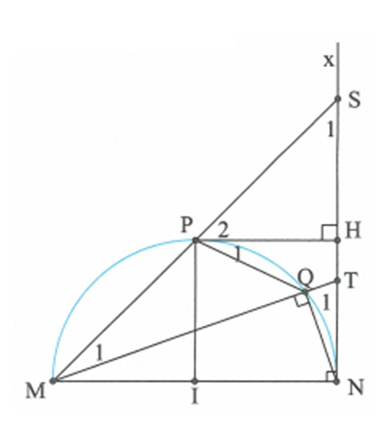
Tam giác MPI có: PI $⊥$ MN (vì P là điểm chính giữa của đường tròn (O));

IP = IM (bán kính đường tròn (O)).

Suy ra $∆$ MPI vuông cân tại I nên MPI = IMP = 45 $°$ .

Tam giác vuông SMN có SMN = 45 $°$ nên $∆$ SMN vuông cân tại N. Do đó MN = SN.

Câu 5/6

b) Chứng minh tam giác MNT đồng dạng với tam giác NQT.

Xem đáp án

Lời giải

Xét $∆$ MNT và $∆$ NQT có:

MNT = NQT = 90 $°$ (giả thiết);

MTN chung.

Suy ra $∆$ MNT đồng dạng $∆$ NQT.

Câu 6/6

c) Chứng minh tứ giác PQTS nội tiếp được trong một đường tròn.

Xem đáp án

Lời giải

Ta có T₁= S₁ (góc ngoài của $∆$ TMS). (1)

Kẻ tiếp tuyến PH ( P $\in$ Nx) . Ta có PH // MN (vì cùng vuông góc với PI), suy ra $∆$ PHS vuông cân tại H => S₁= P₂.

Mặt khác M₁= P₁ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn PQ).

=> M₁ + S₁= P₁ + P₂ = SPQ (2)

Từ (1) và (2) suy ra T₁ = SPQ.

Mà T₁ là góc ngoài tại đỉnh đối diện với đỉnh P nên tứ giác PQTS nội tiếp.

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Cho tam giác ABC vuông tại A. Kẻ đường cao AH và phân giác trong AD của góc HAC. Phân giác trong góc ABC cắt AH, AD lần lượt tại M, N. Chứng minh rằng BND = 90 $°$ .

Cho tam giác ABC cân tại A và nội tiếp trong đường tròn tâm O, đường kính AI. Gọi E là trung điểm của AB, K là trung điểm của OI, H là trung điểm của EB.

a) Chứng minh HK $⊥$ AB.