Chủ đề 1: Vectơ trong không gian

Thi Online Bài tập chuyên đề Toán 11 Bài 1: Vecto trong không gian - Hai đường thẳng vuông góc có đáp án

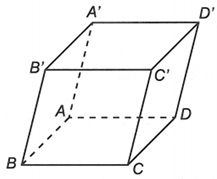
Chủ đề 1: Vectơ trong không gian

670 lượt thi
48 câu hỏi
60 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng $\vec{A C} + \vec{B D} = \vec{A D} + \vec{B C} = 2 \vec{M N}$

Xem đáp án

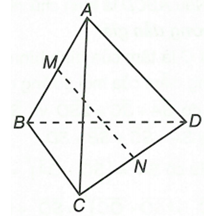
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng vectơ AC (ảnh 1)

Ta có $\vec{A C} + \vec{B D} = \vec{A D} + \vec{B C}$

$\Leftrightarrow \vec{A C} - \vec{A D} = \vec{B C} - \vec{B D}$

$\Leftrightarrow \vec{D C} = \vec{D C}$ (đẳng thức này đúng).

Do M, N lần lượt là trung điểm các cạnh AB và CD

nên $\{\begin{cases} \vec{A M} + \vec{B M} = 0 \\ \vec{N C} + \vec{N D} = 0 \end{cases}$

Do đó $\vec{A D} + \vec{B C} = (\vec{A M} + \vec{M N} + \vec{N B}) + (\vec{B M} + \vec{M N} + \vec{N D})$

$= (\vec{A M} + \vec{B M}) + (\vec{N B} + \vec{N D}) + 2 \vec{M N} = 2 \vec{M N}$

Vậy $\vec{A C} + \vec{B D} = \vec{A D} + \vec{B C} = 2 \vec{M N}$

Câu 2:

Cho hình hộp ABCD.A'B'C'D'. Sử dụng các đỉnh của hình hộp làm điểm đầu và điểm cuối của vectơ.

a) Hãy kể tên các vectơ bằng nhau lần lượt bằng các vectơ $\vec{A B}, \vec{A C}, \vec{A D}, \vec{A A^{'}}$

Xem đáp án

a) Ta có

Cho hình hộp ABCD.A'B'C'D'. Sử dụng các đỉnh của hình hộp làm điểm đầu và điểm cuối của (ảnh 1)

+) $\vec{A B} = \vec{D C} = \vec{A^{'} B^{'}} = \vec{D^{'} C^{'}}$

+) $\vec{A C} = \vec{A^{'} C^{'}}$

+) $\vec{A D} = \vec{B C} = \vec{A^{'} D^{'}} = \vec{B^{'} C^{'}}$

+) $\vec{A A^{'}} = \vec{B B^{'}} = \vec{C C^{'}} = \vec{D D^{'}}$

Câu 3:

Hãy kể tên các vectơ luôn có độ dài bằng nhau và bằng độ dài của vectơ $\vec{B C}$ .

Xem đáp án

Từ tính chất của hình bình hành, ta suy ra các vectơ luôn có độ dài bằng độ dài của vectơ $\vec{B C}$ là $\vec{B C}, \vec{C B}, \vec{A D}, \vec{D A}, \vec{A^{'} D^{'}}, \vec{D^{'} A^{'}}, \vec{B^{'} C^{'}}, \vec{C^{'} B^{'}}$

Câu 4:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.

a) Chứng minh $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Xem đáp án

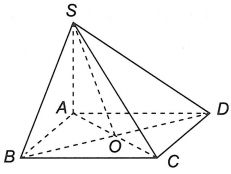
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. a) Chứng minh vectơ SA + vectơ SC (ảnh 1)

a) Gọi O là tâm của hình bình hành ABCD thì O là trung điểm của mỗi đường chéo AC và BD.

Do đó $\vec{S A} + \vec{S C} = 2 \vec{S O}$ và $\vec{S B} + \vec{S D} = 2 \vec{S O}$

Vậy $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$

Câu 5:

b) Nếu ABCD là hình chữ nhật thì ${\vec{S A}}^{2} + {\vec{S C}}^{2} = {\vec{S B}}^{2} + {\vec{S D}}^{2}$

Xem đáp án

b) Ta có ${\vec{S A}}^{2} = {(\vec{S O} + \vec{O A})}^{2} = {\vec{S O}}^{2} + {\vec{O A}}^{2} + 2 \vec{S O} . \vec{O A}$ ,

${\vec{S C}}^{2} = {(\vec{S O} + \vec{O C})}^{2} = {\vec{S O}}^{2} + {\vec{O C}}^{2} + 2 \vec{S O} . \vec{O C}$

Suy ra ${\vec{S A}}^{2} + {\vec{S C}}^{2} = 2 {\vec{S O}}^{2} + {\vec{O A}}^{2} + {\vec{O C}}^{2} + 2 \vec{S O} (\vec{O A} + \vec{O C})$

$= 2 ({\vec{S O}}^{2} + {\vec{O A}}^{2})$ (vì $\vec{O A}$ và $\vec{O C}$ là hai vectơ đối nhau nên $\vec{O A} + \vec{O C} = \vec{0}$ )

$= 2 (S O^{2} + O A^{2})$

Tương tự ${\vec{S B}}^{2} + {\vec{S D}}^{2} = 2 (S O^{2} + O B^{2})$

Mà ABCD là hình chữ nhật nên OA = OB

Suy ra ${\vec{S A}}^{2} + {\vec{S C}}^{2} = {\vec{S B}}^{2} + {\vec{S D}}^{2}$

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan

Các bài thi hot trong chương

Đánh giá trung bình

Thi Online Bài tập chuyên đề Toán 11 Bài 1: Vecto trong không gian - Hai đường thẳng vuông góc có đáp án