Các dạng bài tập vận dụng có đáp án

Câu 1

Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N lần lượt là điểm đối xứng với H qua AB, AC. E, D là hình chiếu của H lên AB, AC. Chứng minh rằng MN là tiếp tuyến của đường tròn đường kính BC.

Xem đáp án

Lời giải

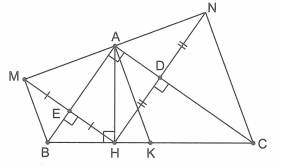
Media VietJack

Ta có: $\hat{B M A} = \hat{B M E} + \hat{A M E} = \hat{B H E} + \hat{A H E} = 90 °$ .

Tương tự ta có: $\hat{A N C} = 90 °$ .

$\hat{M A N} = \hat{M A B} + \hat{B A C} + \hat{C A N} = 2 \hat{B A C} = 180 °$ .

$\Rightarrow M, A, N$ thẳng hàng.

Gọi K là trung điểm của BC. Xét tứ giác BMNC có $M B // N C$ (cùng vuông góc với MN) nên BMNC là hình thang.

Lại có AM = AH =AN (tính chất đối xứng) nên A là trung điểm của MN.

Suy ra KA là đường trung bình của hình thang nên $K A ⊥ M N$ tại A. Do đó MN là tiếp tuyến của đường tròn đường kính BC.

Câu 2

Cho đường tròn (O) đường kính AB có Ax, By là 2 tia tiếp tuyến của (O) (Ax, By) cùng nằm trên nửa mặt phẳng bờ là đường thẳng AB). Trên tia Ax lấy điểm C sao cho $\hat{C O D} = 90$ . Chứng minh rằng CD tiếp xúc với đường tròn (O).

Xem đáp án

Lời giải

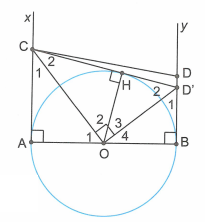
Media VietJack

Từ C vẽ tiếp tuyến CD’ của đường tròn (O) (D’ thuộc By) tiếp xúc với (O) tại tiếp điểm H.

Theo tính chất hai tiếp tuyến cắt nhau ta có: OC là phân giác của $\hat{A O H}$ và OD’ là phân giác của $\hat{B O H}$ .

Mà hai góc $\hat{A O H}$ và $\hat{B O H}$ là hai góc kề bù nên $\hat{C O D^{'}} = 90 °$ .

Mà theo giả thiết $\hat{C O D} = 90 °$ và D, D’ đều thuộc By nên suy ra D’ = D.

Vì CD’ là tiếp tuyến của (O) nên CD cũng là tiếp tuyến của (O).

Câu 3

Cho đường tròn (O; R) đường kính AB. Vẽ dây AC sao cho $\hat{C A B} = 30 °$ . Trên tia đối của tia BA, lấy điểm M sao cho B là trung điểm của OM. Chứng minh rằng:

a) MC là tiếp tuyến của đường tròn (O).

b) $M C^{2} = 3 R^{2}$ .

Xem đáp án

Lời giải

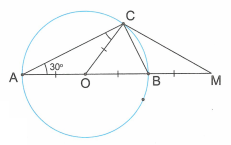
Media VietJack

a) Ta có: $\hat{C O B} = \hat{C A O} + \hat{A C O} = 2 \hat{C A O} = 60 °$ (góc ngoài của $Δ A C O$ ).

Suy ra $Δ C O B$ là tam giác đều.

$\Rightarrow C B = O B = B M \Rightarrow Δ C O M$ vuông tại C hay $O M ⊥ O C$ .

Vậy MC là tiếp tuyến của đường tròn (O).

b) Áp dụng định lí Pytago trong tam giác vuông OMC có:

$O M^{2} = O C^{2} + C M^{2} \Rightarrow C M^{2} = O M^{2} - O C^{2} = {(2 R)}^{2} - R^{2} = 3 R^{2}$ .

Câu 4

Cho tam giác ABC vuông tại A có AB = 8, AC = 15. Vẽ đường cao AH. Gọi D là điểm đối xứng với B qua H. Vẽ đường tròn đường kính CD, cắt AC ở E.

a) Chứng minh rằng HE là tiếp tuyến của đường tròn.

b) Tính độ dài HE.

Xem đáp án

Lời giải

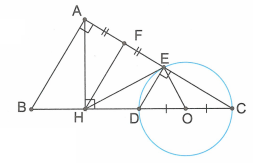
Media VietJack

a) Gọi O là trung điểm của CD.

Vì tam giác DEC có một cạnh DC là đường kính của đường tròn (O) nên $\hat{D E C} = 90 °$ .

Kẻ $H F ⊥ A C \Rightarrow B A // H F // E D \Rightarrow A F = E F$

$\Rightarrow Δ A H E$ cân tại H $\Rightarrow \hat{H A E} = \hat{H E A}$ (hai góc đáy).

Mà $\hat{H A E} = \hat{A B H}$ (vì cùng phụ với $\hat{H A B}$ ).

Suy ra $\hat{H E A} = \hat{A B H}$ . (1)

Mặt khác ta cũng có $\hat{O E C} = \hat{O C E}$ (do $Δ E O C$ cân tại O). (2)

Từ (1) và (2) ta có

$\hat{A B H} + \hat{A C H} = 90 ° \Rightarrow \hat{A E H} + \hat{C E O} = 90 ° \Rightarrow \hat{H E O} = 90$ hay HK là tiếp tuyến của (O).

b) Áp dụng định lí Pytago trong tam giác vuông ABC ta được:

$B C^{2} = A B^{2} + A C^{2} = 8^{2} + 15^{2} = 289 \Rightarrow B C = 17$ .

Áp dụng hệ thức lượng trong tam giác vuông ABC ta được:

$A H . B C = A B . A C \Rightarrow A H = \frac{A B . A C}{B C} = \frac{8.15}{17} = \frac{120}{17}$ .

Do $Δ H A E$ cân tại H nên $H E = A H = \frac{120}{17}$ .

Câu 5

Từ một điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB với đường tròn. Trên tia OB lấy điểm C sao cho BC = BO. Chứng minh rằng $\hat{B M C} = \frac{1}{2} \hat{B M A}$ .

Xem đáp án

Lời giải

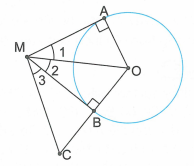
Media VietJack

Ta có: $\hat{M_{1}} = \hat{M_{2}}$ (tính chất hai tiếp tuyến cắt nhau).

$\hat{M_{2}} = \hat{M_{3}}$ (do $Δ C M O$ cân tại M).

$\Rightarrow \hat{M_{1}} = \hat{M_{2}} = \hat{M_{3}} = \frac{1}{2} \hat{A M B}$ ,

$\Rightarrow \hat{B M C} = \frac{1}{2} \hat{B M A}$ ,

Câu 6