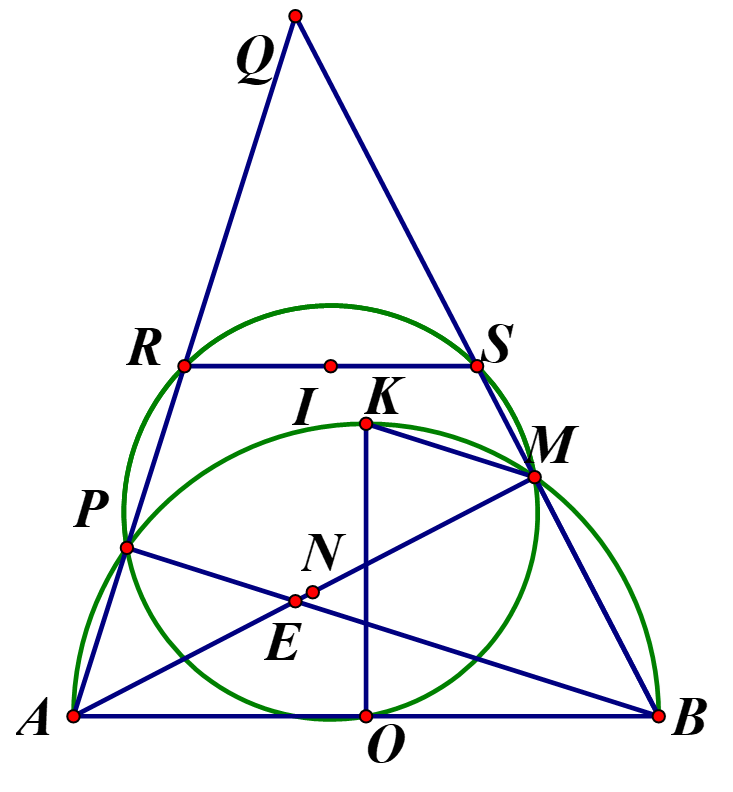
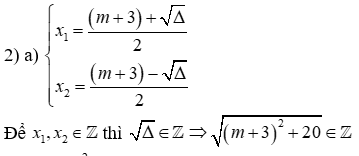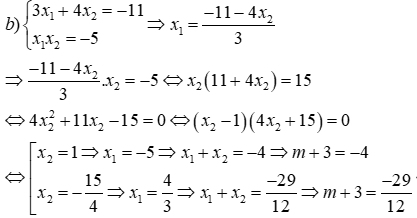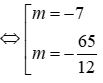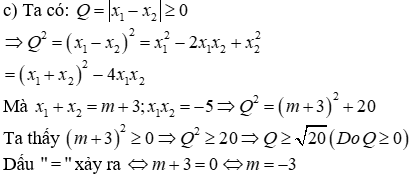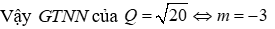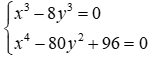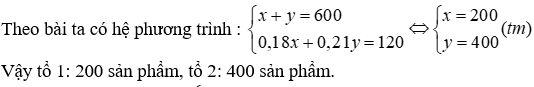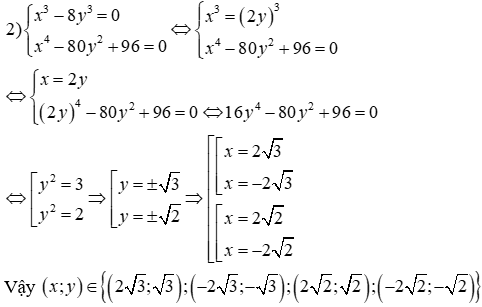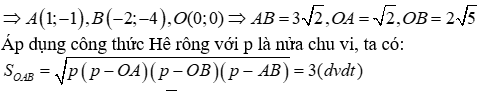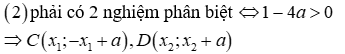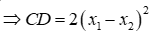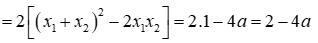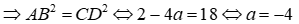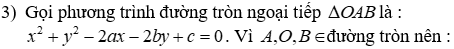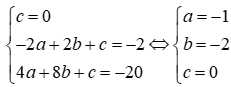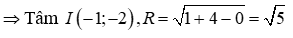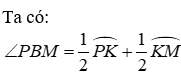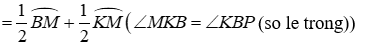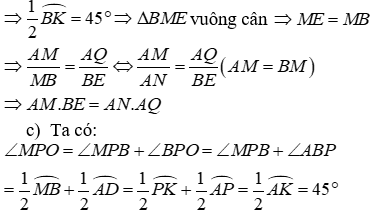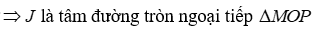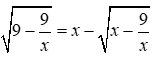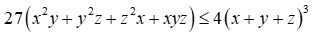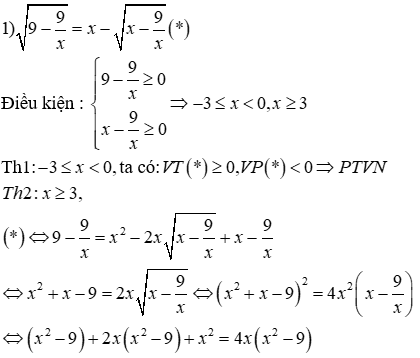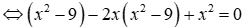Đề thi Giữa học kỳ 2 Toán 9 - Đề 70 có đáp án
31 người thi tuần này 4.6 15 K lượt thi 5 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
169 người thi tuần này
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
338 lượt thi
36 câu hỏi
132 người thi tuần này
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
264 lượt thi
15 câu hỏi
108 người thi tuần này
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
216 lượt thi
19 câu hỏi
92 người thi tuần này
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
184 lượt thi
15 câu hỏi
93 người thi tuần này
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
186 lượt thi
6 câu hỏi
93 người thi tuần này
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
186 lượt thi
3 câu hỏi
97 người thi tuần này
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
194 lượt thi
20 câu hỏi