20 câu Chuyên đề Toán 12 Bài 4: Giá trị lớn nhất và giá trị nhỏ nhất của môđun số phức có đáp án
42 người thi tuần này 4.6 3.7 K lượt thi 20 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Chọn B
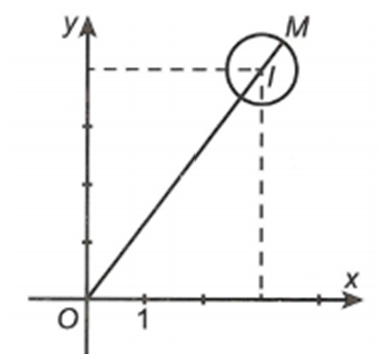
Gọi M(x;y), I(3;4) là các điểm biểu diễn lần lượt cho các số phức z; 3 + 4i. Từ giả thiết
Tập hợp các điểm M biểu diễn số phức z thỏa mãn giả thiết là đường tròn tâm I(3;4), bán kính r = 1.
Mặt khác . Mà OM đạt giá trị lớn nhất bằng OI + r, khi M là giao điểm của đường thẳng OM với đường tròn tâm I(3;4), bán kính r. Hay
Do đó, , khiCâu 2
A. z = 2 - 2i
B. z = 1 + i
C. z = 2 + 2i
D. z = 1 - i
Lời giải
Chọn C
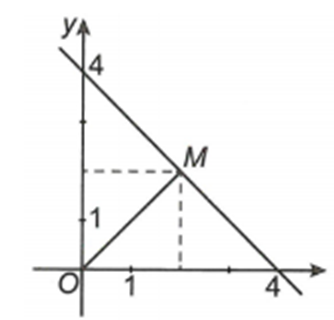
Đặt . Khi đó
Vậy tập hợp điểm M biểu diễn số phức z là đường thẳng d
Do đó nhỏ nhất khi M là hình chiếu của O trên d
Suy ra M(2;2) hay z = 2 + 2i
Lời giải
Chọn B
Gọi có trung điểm là O(0;0). Điểm M biểu diễn số phức z
Theo công thức trung tuyến thì
Ta có
Đẳng thức xảy ra khi
Khi z = 4i hoặc z = -4i
Lời giải
Chọn D
Gọi A(0;-1), B(0;1) đoạn thẳng AB có trung điểm O(0;0) . Điểm M biểu diễn số phức z
Theo công thức trung tuyến
Theo giả thiết . Đặt
Khi đó
Ta có
Do nên
Đẳng thức khi . Đẳng thức khi
Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của làLời giải
Chọn D
Đặt
Gọi lần lượt là các điểm biểu diễn các số phức
Do M, N là điểm biểu diễn số phức và nên suy ra M, N đối xứng nhau qua Ox.
Khi đó
Ta có . Theo giả thiết ta có , tập hợp điểm M thỏa điều kiện trên là elip có trục lớn ; trục bé
Nên elip có phương trình
Do đó
Đẳng thức xảy ra khiLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A.
B.
C. a = 1
D. a = 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. z = 1 + 2i
B. z = -1 - i
C. z = 2 + 2i
D. z = -1 + i
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. 9
B. 10
C. 11
D. 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A.
B. maxT = 4
C.
D. maxT = 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.