Bộ 24 Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 12)
25 người thi tuần này 4.6 23.7 K lượt thi 5 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
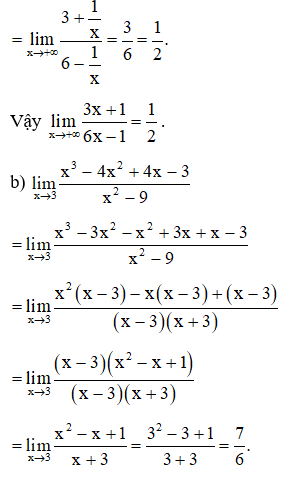
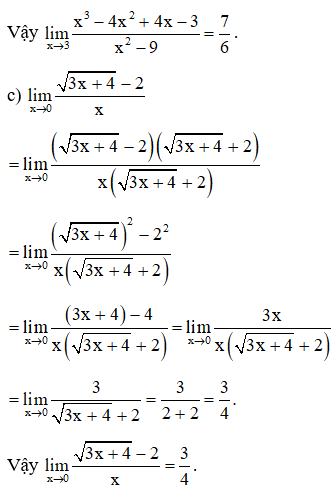
Lời giải
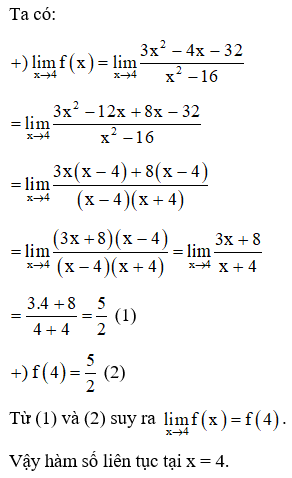
Lời giải
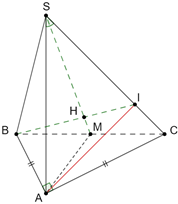
a) Ta có: SA ^ (ABC) suy ra SA ^ BC.
Tam giác ABC vuông cân tại A với M là trung điểm của BC nên suy ra AM ^ BC
Do đó BC ^ (SAM).
b) Ta có CA ^ AB và do SA ^ (ABC) nên SA ^ AC.
Do đó AC ^ (SAB).
Vậy góc giữa đường thẳng SC và mặt phẳng (ABC) là góc .
Ta có:
Do đó .
c) Ta có
+) BC ^ (SAM) Þ BC ^ SM (1)
+) BA ^ SA và BA ^ AC nên suy ra BA ^ (SAC) Þ BA ^ SC
Lại có AI ^ SC.
Nên suy ra SC ^ (BAI) Þ SC ^ BI (2)
Từ (1) và (2), xét trong tam giác SBC nên H là trực tâm của tam giác SBC.
Lời giải
Ta có a.cos4 x + b.cos3 x - 2c.cos x = 2a.sin3 x.
Xét hàm số f (x) = a.cos4 x + b.cos3 x - 2c.cos x - 2a.sin3 x.
+) Với a = 0 Þ f (x) = b.cos3 x - 2c.cos x = cos x.( b.cos2 x - 2c) = 0
Nên luôn cho nghiệm cos x = 0 (*)
+) Với a ¹ 0 Þ f (x) = a.cos4 x + b.cos3 x - 2c.cos x - 2a.sin3 x
f (x) liên tục trên ℝ nên liên tục trên đoạn (1)
Ta có:
(2)
Từ (1) và (2) nên suy ra phương trình f (x) = 0 có ít nhất một nghiệm thuộc khoảng (**)
Từ (*) và (**), vậy suy ra phương trình a.cos4 x + b.cos3 x - 2c.cos x = 2a.sin3 x luôn có nghiệm với mọi tham số a, b, c.