Đề số 10

🔥 Học sinh cũng đã học

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm 9 trường THPT Phú Thọ có đáp án

0 lượt thi 22 câu hỏi

46 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Lào Cai có đáp án

92 lượt thi 22 câu hỏi

33 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Trường THPT Ngô Quyền (Hải Phòng) có đáp án

66 lượt thi 22 câu hỏi

33 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Quảng Ninh có đáp án

66 lượt thi 22 câu hỏi

27 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 ĐH KHTN Hà Nội lần 2 có đáp án

54 lượt thi 22 câu hỏi

31 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Hưng Yên lần 1 có đáp án

62 lượt thi 22 câu hỏi

29 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Ninh Bình lần 2 có đáp án

58 lượt thi 22 câu hỏi

23 người thi tuần này

Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm 5 các trường THPT Ninh Bình có đáp án

46 lượt thi 22 câu hỏi

Danh sách câu hỏi:

Câu 1/50

Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a. Thể tích của khối nón đã cho bằng

\frac{2 π a^{3}}{3}

\frac{\sqrt{3} π a^{3}}{3}

\frac{π a^{3}}{3}

\frac{\sqrt{3} π a^{3}}{2}

Lời giải

Đáp án B

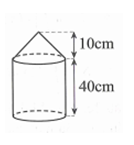
Gọi h là chiều cao khối nón ta có: $h = \sqrt{{(2 a)}^{2} - a^{2}} = a \sqrt{3}$ .

Vậy thể tích khối nón là:

V = \frac{1}{3} π a^{2} . a \sqrt{3} = \frac{\sqrt{3} π a^{3}}{3}

Câu 2/50

Cho hàm số f(x) có đồ thị f'(x) như hình vẽ. Số điểm cực trị của hàm số f(x) là

A. 3.

B. 4.

C. 2.

D. 1.

Lời giải

Đáp án C

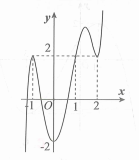
Ta có f'(x) chỉ đổi dấu khi qua $x = - 1; x = 3$ do đó hàm số f(x) chỉ có hai điểm cực trị $x = - 1; x = 3$ .

Câu 3/50

Trong không gian với hệ trục tọa độ Oxyz, cho A(0;-1;1), B(-2;1;-1), C(-1;3;2) . Biết rằng ABCD là hình bình hành, khi đó tọa độ điểm D là

D (1; 1; 4)

D (- 1; 1; \frac{2}{3})

D (1; 3; 4)

D (- 1; - 3; - 2)

Lời giải

Đáp án A

Gọi tọa độ điểm $D (x; y; z)$ .

Ta có: $\{\begin{cases} \vec{A B} = (- 2; 2; - 2) \\ \vec{D C} = (- 1 - x; 3 - y; 2 - z) \end{cases}$ .

Vì ABCD là hình bình hành nên $\vec{A B} = \vec{D C}$ .

Do đó, ta có hệ sau: $\{\begin{cases} - 1 - x = - 2 \\ 3 - y = 2 \\ 2 - z = - 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 1 \\ z = 4 \end{cases}$ .

Vậy tọa độ điểm $D (1; 1; 4)$ .

Câu 4/50

Cho hàm số f(x) có bảng biến thiên như sau:

Hàm số đồng biến trên khoảng nào dưới đây?

(- \infty; 1)

(- 1; + \infty)

(0; 1)

(- \infty; 0)

Lời giải

Đáp án D

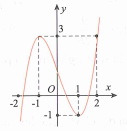
Ta thấy trên khoảng $(- \infty; 0)$ thì $y^{'} > 0$ , suy ra hàm số đồng biến trên khoảng $(- \infty; 0)$ .

Câu 5/50

Tập xác định của hàm số $y = {(x^{3} + x - 6)}^{- \frac{1}{3}}$ là?

D = (- 3; 2)

D = (- \infty; - 3] \cup (2; + \infty)

D = (- \infty; - 3) \cup (2; + \infty)

D = (- \infty; - 3) \cup [2; + \infty)

Lời giải

Đáp án C

Hàm số $y = {(x^{2} + x - 6)}^{- \frac{1}{3}}$ xác định khi và chỉ khi $x^{2} + x - 6 > 0$ .

$\Leftrightarrow (x - 2) (x + 3) > 0 \Leftrightarrow [\begin{array}{l} x < - 3 \\ x > 2 \end{array}$ .

Vậy tập xác định của hàm số đã cho là $D = (- \infty; - 3) \cup (2; + \infty)$ .

Câu 6/50

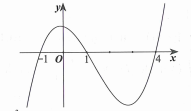
Cho hàm số f(x) liên tục trên đoạn [-1;4] và có đồ thị trên đoạn [-1;4] như hình vẽ bên. Tích phân $\int_{- 1}^{4} f (x) d x$ bằng

\frac{5}{2}

\frac{11}{2}

C. 5.

D. 3.

Lời giải

Đáp án A

Ta có $\int_{- 1}^{4} f (x) d x = \int_{- 1}^{2} f (x) d x + \int_{2}^{4} f (x) d x$

Trong đó $\int_{- 1}^{2} f (x) d x = \int_{- 1}^{2} |f (x)| d x = \frac{(1 + 3) .2}{2} = 4$

Và $\int_{2}^{4} f (x) d x = - \int_{2}^{4} f (x) d x = - \frac{(1 + 2) .1}{2} = \frac{3}{2}$ .

Vậy $\int_{- 1}^{4} f (x) d x = 4 - \frac{3}{2} = \frac{5}{2}$ .

Câu 7/50

Thể tích của khối cầu bán kính a bằng

\frac{4 π a^{3}}{3}

4 π a^{3}

\frac{π a^{3}}{3}

2 π a^{3}

Lời giải

Đáp án A

Thể tích khối cầu bán kính a là $V = \frac{4}{3} π a^{3}$ .

Câu 8/50

Tìm nghiệm phương trình $3^{x - 1} = 9$ .

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải

Đáp án C

Ta có: $3^{x - 1} = 9 \Leftrightarrow 3^{x - 1} = 3^{2} \Leftrightarrow x = 3$ .

Câu 9/50

Trong không gian với hệ trục tọa độ Oxyz, gọi $(α)$ là mặt phẳng đi qua điểm A(2;-1;1) và song song với mặt phẳng(Q):2x-y+3z+2=0 . Phương trình mặt phẳng $(α)$ là.

4 x - 2 y + 6 z + 8 = 0

2 x - y + 3 z - 8 = 0

2 x - y + 3 z + 8 = 0

4 x - 2 y + 6 z - 8 = 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10/50

Mệnh đề nào sau đây là đúng?

\int x e^{x} d x = e^{x} + x e^{x} + C

B. $. \int x e^{x} d x = \frac{x^{2}}{2} e^{x} + e^{x} + C$

\int x e^{x} d x = x e^{x} - e^{x} + C

\int x e^{x} d x = \frac{x^{2}}{2} e^{x} + C

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11/50

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng D song song với đường thẳng $(d) : \{\begin{cases} x = 2 - t \\ y = 1 \\ z = - 1 + 3 t \end{cases}$ . Một véctơ chỉ phương của D là:

\vec{a} (2; 0; - 6)

\vec{b} (- 1; 1; 3)

\vec{v} (2; 1; - 1)

\vec{u} (1; 0; 3)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12/50

Một nhóm học sinh gồm 9 nam và 6 nữ. Giáo viên cần chọn 1 học sinh làm trực nhật. Hỏi có bao nhiêu cách chọn?

A. 3

B. 15.

C. 9.

D. 6.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13/50

Cho một cấp số cộng có $u_{4} = 2, u_{2} = 4$ . Hỏi $u_{1}$ bằng bao nhiêu?

u_{1} = 6

u_{1} = 1

u_{1} = 5

u_{1} = - 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14/50

Gọi và lần lượt là các điểm biểu diễn cho các số phức z và $\bar{z}$ . Xác định mệnh đề đúng.

A. M và M' đối xứng nhau qua trục hoành

B. M và M' đối xứng nhau qua trục tung.

C. M và M' đối xứng nhau qua gốc tọa độ

D. Ba điểm O,M và M' thẳng hàng

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15/50

Đồ thị trong hình vẽ bên dưới là của hàm số nào sau đây?

y = {(x + 1)}^{3}

y = {(x - 1)}^{3}

y = x^{3} - 1

y = x^{3} + 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16/50

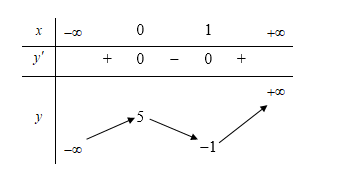
Xét hàm số $y = f (x)$ với $x \in [- 1; 5]$ có bảng biến thiên như sau:

Khẳng định nào sai đây là đúng

A. Hàm số đã cho không tồn tại GTLN trên

[- 1; 5]

B. Hàm số đã cho đạt GTNN tại x=-1 và x=2 trên

[- 1; 5]

C. Hàm số đã cho đạt GTNN tại x=-1 và đạt GTLN tại x=5 trên

[- 1; 5]

D. Hàm số đã cho đạt GTNN tại x=0 trên

[- 1; 5]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17/50

Cho hàm số y=f(x) có đạo hàm $f^{'} (x) = (x^{2} - 1) {(x - 3)}^{2019} {(x + 2)}^{2020}, \forall x \in ℝ$ . Số điểm cực tiểu của hàm số đã cho là

A. 5.

B. 4.

D. 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18/50

Cho số phức $z = a + b i (a; b \in ℝ)$ . Tìm phần thực và phần ảo của số phức $z^{2}$ .

A. Phần thực bằng

a^{2} + b^{2}

và phần ảo bằng

2 a^{2} b^{2}

B. Phần thực bằng $a^{2} - b^{2}$ và phần ảo bằng $2 a b$ .

C. Phần thực bằng

a + b

và phần ảo bằng

a^{2} b^{2}

D. Phần thực bằng

a - b

và phần ảo bằng ab.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19/50

Trong không gian với hệ tọa độ Oxyz, mặt cầu có tâm I(1;1;1) và diện tích bằng $4 π$ có phương trình là

{(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 4

B. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 1$ .

{(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 4

{(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20/50

Cho $a = \log_{49} 11$ và $b = \log_{2} 7$ , thì $P = \log_{\sqrt[3]{7}} \frac{121}{8}$ bằng?

P = 12 a + \frac{9}{b}

P = 12 a - \frac{9}{2 b}

P = 12 a - \frac{9}{b}

P = 12 a + \frac{9}{2 b}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 42/50 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tiếng Anh

Công nghệ

Tin học

ĐHQG Hà Nội

ĐHQG Hồ Chí Minh

ĐH Bách Khoa Hà Nội

ĐHSP Hà Nội

Bộ Công an

Bộ Quốc phòng

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Global success

iLearn Smart World

Friends Global

Bright

Explore new worlds

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý