Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 20)

Thi Online Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 20)

8513 lượt thi
50 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Tính giới hạn $\lim \frac{5^{n} - 3^{n}}{5^{n} - 4}$

A. -3

B. 0

C. 5

D. 1

Xem đáp án

Ta có $\lim \frac{5^{n} - 3^{n}}{5^{n} - 4} = \lim \frac{1 - {(\frac{3}{5})}^{n}}{1 - 4. {(\frac{1}{5})}^{n}} = \frac{1 - 0}{1 - 4.0} = 1$

Câu 2:

Cho hai đường thẳng a,b phân biệt và mặt phẳng P . Mệnh đề nào sau đây sai?

A. Nếu $(P) // (Q)$ và $b ⊥ (P)$ thì $b ⊥ (Q)$ .

B. Nếu

a // (P)

và

b ⊥ a

thì

b ⊥ a

C. Nếu

a // (P)

và

b ⊥ (P)

thì

b ⊥ a

D. Nếu

a ⊥ (P)

và

b ⊥ (P)

thì

a // b

Xem đáp án

Lời giải

Theo tính chất mối liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng thì đáp án A,C,Dđúng.

Trong đáp án B nếu a,b nằm trong mặt phẳng song song với (P) thì $b // (P)$ . Vậy kết luận ở câu B sai.

Câu 3:

Cho hình chóp S.ABC có $S A ⊥ (A B C)$ ; tam giác ABC đều cạnh a và SA=a. Tìm góc giữa SC và mặt phẳng $(A B C)$ .

A. $60 °$

B. $90 °$

C. $30 °$

D. $45 °$

Xem đáp án

Lời giải

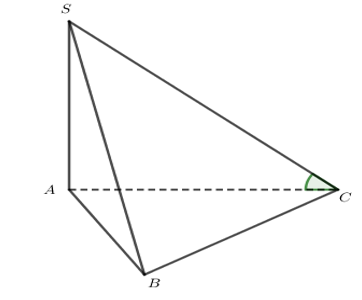
Cho hình chóp S.ABC có SA vuông góc (ABC) ; tam giác ABC đều cạnh a và SA=a. (ảnh 1)

Ta có $C = S C \cap (A B C)$ (1)

Hơn nữa, theo giả thiết $S A ⊥ (A B C)$ nên A là hình chiếu của C lên mặt phẳng (ABC0 (2)

Từ (1) và (2) suy ra AC là hình chiếu vuông góc của SC lên mặt phẳng (ABC).

Khi đó góc giữa SC và mặt phẳng (ABC) là góc giữa SC và AC hay góc $\hat{S C A}$ .

Tính góc $\hat{S C A}$

Ta có $S A ⊥ (A B C)$ mà $A C \subset (A B C)$ nên $S A ⊥ A C$ .

Mặt khác, $S A = A C = a$ ( theo giả thiết).

Suy ra tam giác SAC vuông cân tại A, suy ra $\hat{S C A} = 45^{0}$ .

Câu 4:

Trong các giới hạn sau giới hạn nào bằng 0 ?

A. $\lim \frac{n + 3}{n + 2}$

B. $\lim {(\frac{2019}{2020})}^{n}$

C. $\lim 2^{n}$

D. $\lim n^{4}$

Xem đáp án

Lời giải

Xét đáp án A, $\lim \frac{n + 3}{n + 2} = \lim \frac{1 + 3. \frac{1}{n}}{1 + 2. \frac{1}{n}} = \frac{1 + 3.0}{1 + 2.0} = 1$ .

Xét đáp án B, $\lim {(\frac{2019}{2020})}^{n} = 0$ vì $|\frac{2019}{2020}| < 1$ .

Xét đáp án C, $\lim 2^{n} = + \infty$ .

Xét đáp án D, $\lim n^{4} = + \infty$ .

Câu 5:

Cho tứ diện đều ABCD cạnh a. Tính tích vô hướng $\vec{A B} . \vec{A C}$ theo .

A. $\frac{1}{2} a^{2}$

B. $A^{2}$

C. $- a^{2}$

D. $\frac{\sqrt{3}}{2} a^{2}$

Xem đáp án

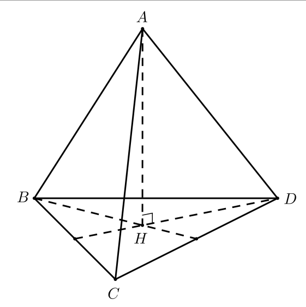
Cho tứ diện đều ABCD cạnh a. Tính tích vô hướng vectơ AB , AC theo . (ảnh 1)

Tứ diện ABCD là tứ diện đều cạnh a nên suy ra tam giác ABC đều cạnh a.

Do đó $\vec{A B} . \vec{A C} = |\vec{A B}| . |\vec{A C}| . \cos (\vec{A B}, \vec{A C}) = A B . A C . \cos \hat{B A C} = a . a . \cos 60 ° = \frac{1}{2} a^{2} .$

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Các bài thi hot trong chương:

Top 4 Đề thi Toán 11 Học kì 2 có đáp án

( 8 K lượt thi )

Đề thi Toán 11 Học kì 2 có đáp án

( 5.6 K lượt thi )

Đề thi Toán lớp 11 Học kì 1 có đáp án

( 8.2 K lượt thi )

Đề thi Toán 11 Học kì 1 có đáp án

( 5.3 K lượt thi )

Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án

( 4.3 K lượt thi )

Đề kiểm tra giữa học kì 1 Toán lớp 11 có đáp án (Mới nhất)

( 4.2 K lượt thi )

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án

( 3.9 K lượt thi )

Đánh giá trung bình

Thi Online Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)