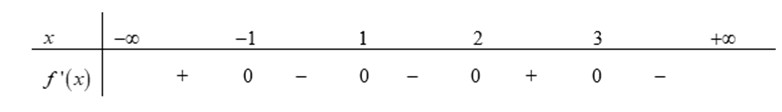30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải - Đề 1
79 người thi tuần này 4.6 19.2 K lượt thi 50 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Thị Minh Khai (Hà Nội) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Liên trường THPT (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Đại học Vinh lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm liên trường Nghệ An có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Bắc Ninh có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên ĐH KHTN Hà Nội lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Hưng Yên có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Gia Thiều (Hà Nội) có đáp án
Danh sách câu hỏi:
Lời giải
Chọn C.
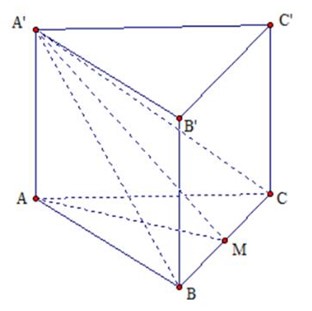
Gọi M là trung điểm của
suy ra
Vậy
Tam giác ABC đều cạnh a nên
Lời giải
Điều kiện:
Từ giả thiết ta có:
Xét hàm số trên
Ta có:
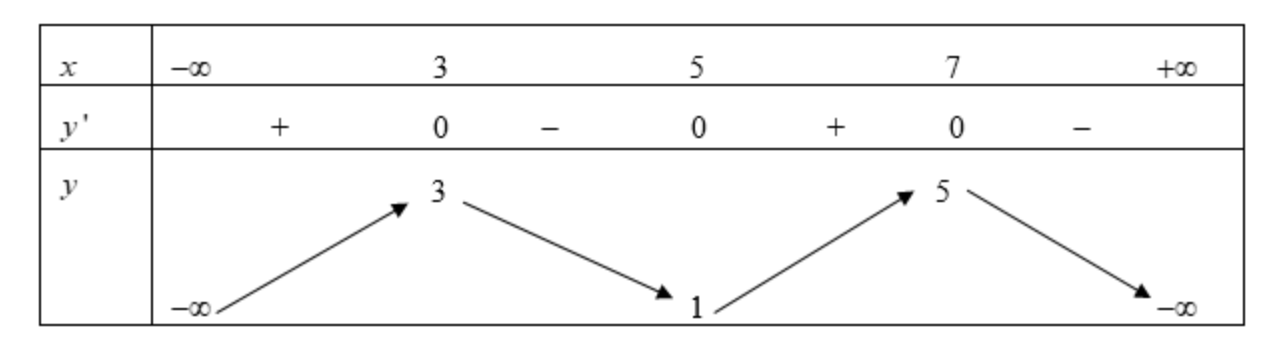
Bảng biến thiên:
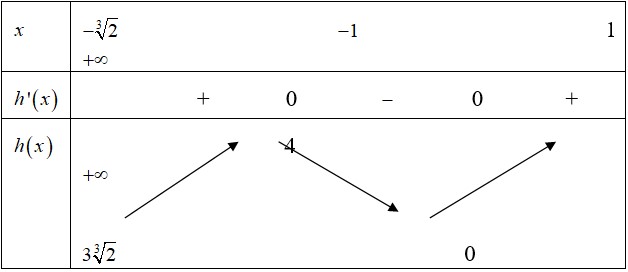
Từ bảng biến thiên suy ra:
Suy ra:
Ta có:
Xét hàm số trên
Ta có:
Ta có:
suy ra hàm số đồng biến trên
Suy ra:
suy ra hàm số đồng biến trên
Vậy Suy ra:
Dấu “=” xảy ra khi và chỉ khi:
Lời giải
Lúc đầu đám vi trùng có 300000 con suy ra
Khi đó
Suy ra
VậyCâu 4
A. 1
B. 4
C. 3
D. 2
Lời giải
Ta có Xét .
Bảng xét dấu:

Từ bảng xét dấu, ta suy ra hàm số có tất cả 3 điểm cực trị.
Câu 5
A. 30.
B. 6.
C. 60.
D. 27.
Lời giải
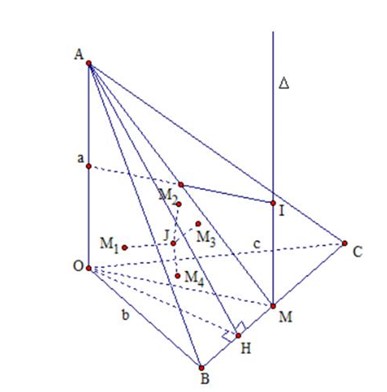
Đặt
Gọi là trung điểm của
dựng trục đường tròn ![]() ngoại tiếp tam giác
ngoại tiếp tam giác
trên mặt phẳng
kẻ đường trung trực của đoạn cắt tại là
tâm mặt cầu ngoại tiếp hình chóp
+)
+) Gọi là chân đường cao hạ từ đỉnh của
tam giác suy ra:
Suy ra:
+) Gọi là tâm mặt cầu nội tiếp hình chóp
Khi đó:
Suy ra:
Vậy Dấu “=” xảy ra khi .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Tập xác định của hàm số là
B. Tập giá trị của hàm số là
C. Tập giá trị của hàm số là
D. Tập xác định của hàm số là
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. x2y=1
B. xy=1
C. 3xy=1
D. x2+3y = 3x
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
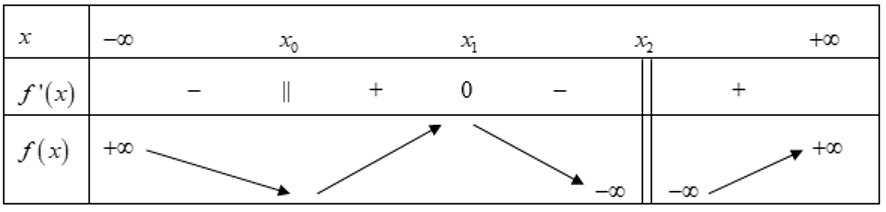
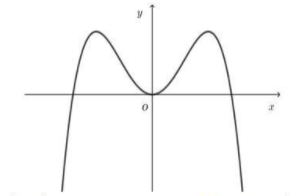
A. Một điểm cực đại, hai điểm cực tiểu.
B. Hai điểm cực đại, một điểm cực tiểu.
C. Một đường tiệm cận đứng và một đường tiệm cận ngang.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. u4 = 12
B. u4 = 13
C. u4 = 36
d. u4 = 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. 7
B. 8
C. 6
D. 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. 1
B. 2
C. 4
D. 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. (-1;-1;0)
B. (1;1;1)
C. (1;4;0)
D. (2;1;0)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. 64cm3
B. 8cm3
C. 2cm3
D. 6cm3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. 1969
B. 1989
C. 1997
D. 2008
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. x=10
B. x= -10
C. x = 10 và x = -10
D. x=10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. Hàm số có tập giá trị là R
B. Hàm số có tập giá trị là
C. Hàm số y=sinx có tập giá trị là
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
A. 165269 (nghìn đồng).
B. 169234 (nghìn đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
A. Trung điểm SD.
B. Trung điểm SB.
C. Điểm nằm trên đường thẳng d//SA và không thuộc SC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 42
C. P=-4
D. P=3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 44
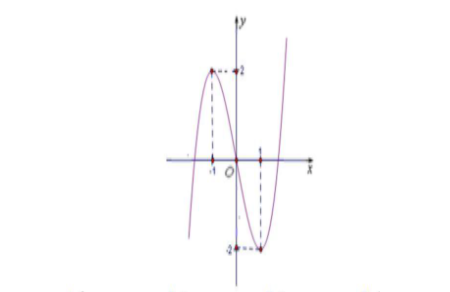
A. f(x)=x4-2x2
B. f(x)=-x4+2x2-1
C. f(x)=-x4+2x2
D. f(x)=x4+2x2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 45
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 48
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.