87 câu Chuyên đề Toán 12 Bài 3 Dạng 5: Một số bài toán cực trị có đáp án

25 người thi tuần này 4.6 32.7 K lượt thi 7 câu hỏi 45 phút

🔥 Học sinh cũng đã học

17 người thi tuần này

Đề KSCL Toán 12 tháng 10 năm 2026-2027 THPT Nguyễn Bỉnh Khiêm (Gia Lai) có đáp án

84 lượt thi 22 câu hỏi

17 người thi tuần này

Đề KSCL Toán 12 tháng 10 năm 2026-2027 THCS&THPT Nguyễn Khuyến - TH-THCS-THPT Lê Thánh Tông (TP HCM) có đáp án

84 lượt thi 22 câu hỏi

14 người thi tuần này

Đề KSCL Toán 12 tháng 8 năm 2026-2027 THCS&THPT Nguyễn Khuyến (TP HCM) có đáp án

81 lượt thi 22 câu hỏi

19 người thi tuần này

Đề KSCL Toán 12 tháng 8 năm 2026-2027 THPT Tạ Quang Bửu (Hà Nội) có đáp án

86 lượt thi 22 câu hỏi

287 người thi tuần này

Đề thi giữa kì 1 Toán 12 năm 2026-2027 THPT Việt Đức (Hà Nội) có đáp án

574 lượt thi 22 câu hỏi

407 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Lê Trọng Tấn (TP.HCM) có đáp án

6 K lượt thi 22 câu hỏi

150 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Thủ Đức (TP.HCM) có đáp án

5.7 K lượt thi 22 câu hỏi

198 người thi tuần này

Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Ngô Quyền (TP.HCM) có đáp án

5.8 K lượt thi 22 câu hỏi

Danh sách câu hỏi:

Câu 1/7

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(-2,-2,1), A(1,2,-3) và đường thẳng $d : \frac{x + 1}{2} = \frac{y - 5}{2} = \frac{z}{- 1}$ .Tìm một vectơ chỉ phương $\vec{u}$ của đường thẳng D đi qua , vuông góc với đường thẳng đồng thời cách điểm một khoảng bé nhất.

A. .B. .C. .D. .

Lời giải

Xét là mặt phẳng qua và .

Mặt phẳng qua và có vectơ pháp tuyến nên có phương trình: .

Gọi lần lượt là hình chiếu của lên và D.

Khi đó nên đạt giá trị nhỏ nhất khi và chỉ khi .

Đường thẳng đi qua và có vectơ chỉ phương nên có phương trình tham số là .

Vì nên .

Lại nên .

Vậy .

Chọn C.

Câu 2/7

Trong không gian Oxyz, cho mặt cầu (S) có phương trình $x^{2} + y^{2} + z^{2} - 4 x + 2 y - 2 z - 3 = 0$ và điểm $A (5; 3; - 2)$ . Một đường thẳng d thay đổi luôn đi qua A và luôn cắt mặt cầu tại hai điểm phân biệt $M, N$ .

Tính giá trị nhỏ nhất của biểu thức $S = A M + 4 A N$ .

A. $S_{\min} = 30$ .

S_{\min} = 20

S_{\min} = 5 \sqrt{34} - 9

S_{\min} = \sqrt{34} - 3

Lời giải

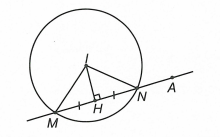
Media VietJack

Mặt cầu $(S)$ có tâm $I (2; - 1; 1)$ , bán kính $R = \sqrt{2^{2} + {(- 1)}^{2} + 1^{2} - (- 3)} = 3$ .

Ta có: $A I = \sqrt{{(2 - 5)}^{2} + {(- 1 - 3)}^{2} + {(1 + 2)}^{2}} = \sqrt{34} > R$ nên A nằm ngoài mặt cầu $(S)$ .

Ta lại có: $S = A M + 4 A N$ .

Đặt $A M = x, x \in [\sqrt{34} - 3; \sqrt{34} + 3]$ .

Mà $A M . A N = A I^{2} - R^{2} = 34 - 9 = 25 \Rightarrow A N = \frac{25}{A M}$ .

Do đó: $S = f (x) = x + \frac{100}{x}$ với $x \in [\sqrt{34} - 3; \sqrt{34} + 3]$ .

Ta có: $f^{'} (x) = 1 - \frac{100}{x^{2}} = \frac{x^{2} - 100}{x} < 0$ với $x \in [\sqrt{34} - 3; \sqrt{34} + 3]$ .

Do đó: $\min_{[\sqrt{34} - 3; \sqrt{34} + 3]} f (x) = f (\sqrt{34} + 3) = 5 \sqrt{34} - 9$ .

Dấu “=” xảy ra $\Leftrightarrow A, M, N, I$ thẳng hàng và $A M = \sqrt{34} + 3; A N = \sqrt{34} - 3$ .

Chọn C.

Câu 3/7

Trong không gian Oxyz, cho hai điểm A(9,6,11), B(5,7,2) và điểm M di động trên mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 36$ .

Giá trị nhỏ nhất của $A M + 2 M B$ bằng

A. $\sqrt{105}$ .

2 \sqrt{26}

2 \sqrt{29}

\sqrt{102}

Lời giải

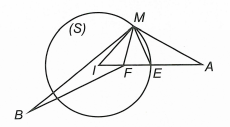
Media VietJack

Mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 36$ có tâm $I (1; 2; 3)$ và bán kính $R = 6$ .

Ta có $I A = 12 = 2 R$ .

Gọi E là giao điểm của IA và mặt cầu $(S)$ suy ra E là trung điểm của IA nên $E (5; 4; 7)$ .

Gọi F là trung điểm của IE suy ra $F (3; 3; 5)$ .

Xét $Δ M I F$ và $Δ A I M$ có $\hat{A I M}$ chung và $\frac{I F}{I M} = \frac{I M}{I A} = \frac{1}{2}$ .

Suy ra $Δ M I F Δ A I M (c.g.c) \Rightarrow \frac{M A}{M F} = \frac{A I}{M I} = 2 \Rightarrow M A = 2 M F$ .

Do đó $A M + 2 M B = 2 (M F + M B) \geq 2 B F = 2 \sqrt{29}$ (theo bất đẳng thức tam giác).

Dấu “=” xảy ra khi M là giao điểm FB và mặt cầu $(S)$ .

Chọn C.

Câu 4/7

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2,-2,4), B(-3,3,-1) và đường thẳng $d : \frac{x - 5}{2} = \frac{y - 2}{- 1} = \frac{z}{- 1}$ . Xét M là điểm thay đổi thuộc d, giá trị nhỏ nhất của $2 M A^{2} + 3 M B^{2}$ bằng

A. 14.

B. 160.

4 \sqrt{10}

D. 18.

Lời giải

Chọn B

Câu 5/7

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1,0,3), B(-3,1,3), C(1,5,1). Gọi $M (x_{0}; y_{0}; z_{0})$ thuộc mặt phẳng tọa độ $(O x y)$ sao cho biểu thức $T = 2 |\vec{M A}| + |\vec{M B} + \vec{M C}|$ có giá trị nhỏ nhất. Giá trị của $x_{0} - y_{0}$ bằng

A. $x_{0} - y_{0} = - \frac{8}{5}$ .

x_{0} - y_{0} = \frac{8}{5}

x_{0} - y_{0} = - 2

x_{0} - y_{0} = 2

Lời giải

Chọn C

Câu 6/7

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1,2,-3),B(-2,-2,1) và mặt phẳng $(α)$ có phương trình $2 x + 2 y - z + 9 = 0$ . Gọi M là điểm thay đổi trên mặt phẳng $(α)$ sao cho M luôn nhìn đoạn AB dưới một góc vuông. Xác định phương trình đường thẳng MB khi MB đạt giá trị lớn nhất.

A. $\{\begin{cases} x = - 2 - t \\ y = - 2 + 2 t \\ z = 1 + 2 t \end{cases}$ .

\{\begin{cases} x = - 2 + 2 t \\ y = - 2 - t \\ z = 1 + 2 t \end{cases}

\{\begin{cases} x = - 2 + t \\ y = - 2 \\ z = 1 + 2 t \end{cases}

\{\begin{cases} x = - 2 + t \\ y = - 2 - t \\ z = 1 \end{cases}

Lời giải

Chọn C

Câu 7/7

Cho mặt cầu $(S) : {(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 3)}^{2} = 9$ và hai điểm $A (1; 1; 3), B (21; 9; - 13)$ .

Điểm $M (a; b; c)$ thuộc mặt cầu $(S)$ sao cho $3 M A^{2} + M B^{2}$ đạt giá trị nhỏ nhất.

Khi đó giá trị của biểu thức $T = a . b . c$ bằng

A. 3.

B. 8.

C. 6.

- 18

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 1/7 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán