Đề thi tuyển sinh vào lớp 10 Toán năm học 2016 - 2017 Sở GD&ĐT Hà Nội có đáp án
63 người thi tuần này 4.6 210 lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
|
1) |
Tính giá trị của biểu thức \(A\) khi \(x = 25\). |
|
Với \(x = 25\) (thỏa mãn điều kiện) thay vào \[A\] ta có: \(A = \frac{7}{{\sqrt {25} + 8}} = \frac{7}{{5 + 8}} = \frac{7}{{13}}\). |
|
|
2) |
Chứng minh \[B = \frac{{\sqrt x + 8}}{{\sqrt x + 3}}\]. |
|
Với \(x \ge 0,x \ne 9\), ta có: \[B = \frac{{\sqrt x }}{{\sqrt x - 3}} + \frac{{2\sqrt x - 24}}{{x - 9}}\] \[ = \frac{{\sqrt x }}{{\sqrt x - 3}} + \frac{{2\sqrt x - 24}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\] \( = \frac{{\sqrt x .\left( {\sqrt x + 3} \right) + 2\sqrt x - 24}}{{\left( {\sqrt x - 3} \right).\left( {\sqrt x + 3} \right)}}\) \[ = \frac{{x + 3\sqrt x + 2\sqrt x - 24}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\] \( = \frac{{x + 5\sqrt x - 24}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\) \( = \frac{{x - 3\sqrt x + 8\sqrt x - 24}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\) \( = \frac{{\sqrt x \left( {\sqrt x - 3} \right) + 8\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\) \( = \frac{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 8} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\) \[ = \frac{{\sqrt x + 8}}{{\sqrt x + 3}}\]. |
|
|
3) |
Tìm \(x\) để biểu thức \(P = A.B\) có giá trị là số nguyên. |
|
Với \(x \ge 0,x \ne 9\), ta có: \(P = A.B\)\( = \frac{7}{{\sqrt x + 8}}.\frac{{\sqrt x + 8}}{{\sqrt x + 3}}\)\( = \frac{7}{{\sqrt x + 3}}\). Do \(x \ge 0\) nên \(P > 0\) Do \(x \ge 0\) nên \[\sqrt x + 3 \ge 3 \Leftrightarrow \frac{7}{{\sqrt x + 3}} \le \frac{7}{3}\] Nên \(0 < P \le \frac{7}{3}\). Để \(P\) có giá trị nguyên thì \(P \in \left\{ {1;2} \right\}\) • Với \(P = 1\) thì \(\frac{7}{{\sqrt x + 3}} = 1 \Leftrightarrow \sqrt x + 3 = 7 \Leftrightarrow \sqrt x = 4 \Leftrightarrow x = 16\left( {tm} \right)\); • Với \(P = 2\) thì \(\frac{7}{{\sqrt x + 3}} = 2 \Leftrightarrow \sqrt x + 3 = \frac{7}{2} \Leftrightarrow \sqrt x = \frac{1}{2} \Leftrightarrow x = \frac{1}{4}\,\left( {tm} \right)\). Vậy \(x \in \left\{ {16;\frac{1}{4}} \right\}\) là giá trị cần tìm. |
Lời giải
|
Gọi chiều rộng của mảnh vườn hình chữ nhật là \(x\) \(\left( {\rm{m}} \right)\) \(\left( {x > 0} \right)\). Vì diện tích của của mảnh vườn hình chữ nhật là \(720\,\,{{\rm{m}}^2}\) nên chiều dài là: \(\frac{{720}}{x}\) (m). Sau khi thay đổi kích thước: Chiều dài của của mảnh vườn hình chữ nhật là: \(\frac{{720}}{x} + 10\) \(\left( {\rm{m}} \right)\). Chiều rộng của của mảnh vườn hình chữ nhật là: \[x - 6\] \(\left( {\rm{m}} \right)\). Vì diện tích của của mảnh vườn hình chữ nhật không đổi nên ta có phương trình: \({\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {x - 6} \right)\left( {\frac{{720}}{x} + 10} \right) = 720\) \( \Leftrightarrow 720 + 10x - \frac{{4320}}{x} - 60 = 720\) \( \Leftrightarrow 10{x^2} - 60x - 4320 = 0\) \( \Leftrightarrow {x^2} - 6x - 432 = 0\) \( \Leftrightarrow {x^2} - 24x + 18x - 432 = 0\) \[ \Leftrightarrow x\left( {x - 24} \right) + 18\left( {x - 24} \right) = 0\] \[ \Leftrightarrow \left( {x - 24} \right)\left( {x + 18} \right) = 0\] \( \Leftrightarrow \left[ \begin{array}{l}x = 24\left( {tm} \right)\\x = - 18\left( {ktm} \right)\end{array} \right.\) Vậy chiều rộng mảnh đất hình chữ nhật đó là \[24\,\,{\rm{m}}\]; chiều dài mảnh đất hình chữ nhật đó là: \(\frac{{720}}{{24}} = 30\)\(\left( {\rm{m}} \right)\). |
Lời giải
|
Giải hệ phương trình \[\left\{ {\begin{array}{*{20}{c}}{\frac{{3x}}{{x - 1}} - \frac{2}{{y + 2}} = 4}\\{\frac{{2x}}{{x - 1}} + \frac{1}{{y + 2}} = 5}\end{array}} \right.\] |
|
ĐK: \(x \ne 1,y \ne - 2\). Đặt \(\left\{ \begin{array}{l}\frac{x}{{x - 1}} = a\\\frac{1}{{y + 2}} = b\end{array} \right.\), khi đó hệ phương trình trở thành: \[\left\{ {\begin{array}{*{20}{c}}{3a - 2b = 4}\\{2a + b = 5}\end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{3a - 2b = 4}\\{4a + 2b = 10}\end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{7a = 14}\\{4a + 2b = 10}\end{array}} \right.\] \[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{2a + b = 5}\end{array} \Leftrightarrow } \right.\left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = 5 - 2a}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = 1}\end{array}} \right.\] Khi đó \(\left\{ \begin{array}{l}\frac{x}{{x - 1}} = 2\\\frac{1}{{y + 2}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\left( {x - 1} \right)\\y + 2 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2x - 2\\y = - 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 1\end{array} \right.\) (thỏa mãn điều kiện) Vậy nghiệm của hệ phương trình là \[\left( {2; - 1} \right)\]. |
Lời giải
|
a.Chứng minh \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m.\) |
|
Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\): \({x^2} = 3x + {m^2} - 1\) \( \Leftrightarrow {x^2} - 3x - {m^2} + 1 = 0\) \(\left( * \right)\) Ta có \(\Delta = {\left( { - 3} \right)^2} - 4.1.\left( { - {m^2} + 1} \right) = 9 + 4{m^2} - 4 = 4{m^2} + 5 > 0,\forall m\) Þ Phương trình \(\left( * \right)\) luôn có hai nghiệm phân biệt với mọi \(m\) Vậy \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m.\) |
|
b.Gọi \[{x_1},{x_2}\] là hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\). Tìm \(m\) để \(\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) = 1.\) |
|
Do \({x_1},{x_2}\) là hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) nên \({x_1},{x_2}\) là hai nghiệm của phương trình \(\left( * \right)\). Theo hệ thức Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}{x_2} = - {m^2} + 1\end{array} \right.\) Ta có: \(\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) = 1 \Leftrightarrow {x_1}{x_2} + {x_1} + {x_2} + 1 = 1\) \( \Leftrightarrow {x_1}{x_2} + \left( {{x_1} + {x_2}} \right) = 0\) \( \Leftrightarrow 3 + \left( { - {m^2} + 1} \right) = 0\) \( \Leftrightarrow {m^2} = 4 \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\). Vậy \(m \in \left\{ {2; - 2} \right\}\). |
Lời giải
|
1) |
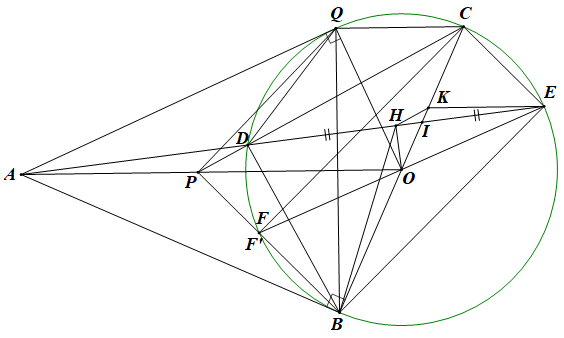
Chứng minh bốn điểm \(A,B,O,H\) cùng nằm trên một đường tròn. |
|
|
|
|
Vì \[AB\] là tiếp tuyến của \[\left( O \right)\] nên \[AB \bot BO\]\( \Rightarrow \widehat {ABO} = 90^\circ \). Vì \(H\) là trung điểm của dây \[DE\] của \[\left( O \right)\] nên \[OH \bot DE\] \( \Rightarrow \widehat {AHO} = 90^\circ \) Suy ra góc \[\widehat {ABO} + \widehat {AHO} = 90^\circ + 90^\circ = 180^\circ \] Mà hai góc này ở vị trí đối nhau trong tứ giác \[AHOB\] Þ tứ giác \[AHOB\] là tứ giác nội tiếp Þ Bốn điểm \[A,H,O,B\] nằm trên cùng một đường tròn. |
|
|
2) |
Chứng minh \[\frac{{AB}}{{AE}} = \frac{{BD}}{{BE}}\]. |
|
Xét \(\left( O \right)\) có \[\widehat {ABD} = \widehat {BED}\] (góc tạo bởi tia tiếp tuyến \(BA\) và dây cung \(BD\) và góc nội tiếp chắn cung \[BD\]) Xét \(\Delta ABD\) và \(\Delta AEB\) có: \(\widehat {BAE}\) là góc chung, \[\widehat {ABD} = \widehat {AEB}\] (do \[\widehat {ABD} = \widehat {BED}\])
\( \Rightarrow \frac{{AB}}{{AE}} = \frac{{BD}}{{BE}}\) (tỉ số đồng dạng). |
|
|
3) |
Đường thẳng \(d\;\) đi qua \(E\) song song với \(AO\), \(d\) cắt \(BC\) tại \(K\). Chứng minh \(HK\,{\rm{//}}\,DC\). |
|
Vì \[ABOH\] là tứ giác nội tiếp nên \[\widehat {OAH} = \widehat {OBH}\] (hai góc nội tiếp cùng chắn cung \(OH\)) Vì \[EK\,{\rm{//}}\,AO\] nên \[\widehat {OAH} = \widehat {HEK}\] (so le trong) Suy ra \[\widehat {OBH} = \widehat {HEK}\], hay \[\widehat {KBH} = \widehat {KEH}\] Mà hai góc này cùng nhìn cạnh \(KH\) trong tứ giác \(BHKE\) \( \Rightarrow BHKE\) là tứ giác nội tiếp \( \Rightarrow \widehat {KHE} = \widehat {KBE}\) (hai góc nội tiếp cùng chắn ). Vì \[BDCE\] là tứ giác nội tiếp nên \[\widehat {CBE} = \widehat {CDE}\] (hai góc nội tiếp cùng chắn ), hay \[\widehat {KBE} = \widehat {CDE}\]. Suy ra \( \Rightarrow \widehat {KHE} = \widehat {CDE}\) Mà hai goc này ở vị trí đồng vị \( \Rightarrow HK\,{\rm{//}}\,DC\). |
|
|
4)
|
Tia \(CD\) cắt \(AO\;\) tại điểm \(P\), tia \(EO\) cắt \(BP\) tại điểm \(F\). Chứng minh tứ giác \(BECF\) là hình chữ nhật. |
|
Gọi \(F'\) là giao điểm của \[BP\] và đường tròn \[\left( O \right)\]. Gọi \[AQ\] là tiếp tuyến thứ hai của \[\left( O \right)\]. Vì \[BDQC\] là tứ giác nội tiếp nên \[\widehat {QDC} = \widehat {QBC}\] (hai góc nội tiếp cùng chắn ). Vì \[ABOQ\] là tứ giác nội tiếp đường tròn đường kính \[AO\] nên \[\widehat {QBO} = \widehat {QAO}\] (hai góc nội tiếp cùng chắn ) hay \[\widehat {QBC} = \widehat {QAO}\] Do đó \[\widehat {QDC} = \widehat {QAO}\] (cùng bằng \(\widehat {QBC}\)) \( \Rightarrow APDQ\) là tứ giác nội tiếp \( \Rightarrow \widehat {PDA} = \widehat {PQA}\) (hai góc nội tiếp cùng chắn ) \(\left( 1 \right)\) Chứng minh \(\Delta ABP = \Delta AQP\left( {c.g.c} \right)\)\[ \Rightarrow \widehat {PQA} = \widehat {PBA}\] \(\left( 2 \right)\) Ta có \(\widehat {PDA} = \widehat {EDC} = \widehat {EBC}\) \(\left( 3 \right)\) Từ \(\left( 1 \right),\left( 2 \right)\) và \(\left( 3 \right)\) suy ra \[\widehat {PBA} = \widehat {EBC}\]. \( \Rightarrow \widehat {ABE} - \widehat {PBA} = \widehat {ABE} - \widehat {EBC}\) \( \Rightarrow \widehat {PBE} = \widehat {ABC} = 90^\circ \). \[ \Rightarrow \widehat {F'BE} = 90^\circ \]\( \Rightarrow F'E\) là đường kính của \[\left( O \right)\] \( \Rightarrow F' \in OE\) \( \Rightarrow F' \equiv F\) hay \(\widehat {FBE} = 90^\circ \) Vì \[FBEC\] là tứ giác nội tiếp nên \(\widehat {FCE} = 180^\circ - \widehat {FBE} = 90^\circ \) Tứ giác \[FBEC\] có \[\widehat {FCE} = \widehat {FBE} = \widehat {BEC{\rm{ }}} = 90^\circ \] nên là hình chữ nhật. |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.