Đề kiểm tra 45 phút Toán 12 Chương 1 Hình học có đáp án (Đề 1)
23 người thi tuần này 4.6 11 K lượt thi 14 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. Chỉ có năm loại hình đa diện đều.
B. Hình hộp chữ nhật có diện tích các mặt bằng nhau là hình đa diện đều.
C. Trọng tâm các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
D. Hình chóp tam giác đều là hình đa diện đều.
Lời giải
Chọn C.
+ Trong không gian ba chiều, có đúng 5 khối đa diện đều lồi, chúng là các khối đa diện duy nhất có tất cả các mặt, các cạnh và các góc ở đỉnh bằng nhau.
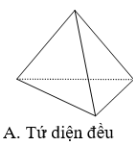
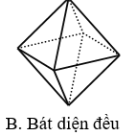
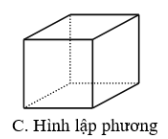
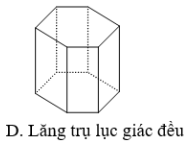
Tứ diện đều | Khối lập phương | Khối bát diện đều | Khối mười hai mặt đều | Khối hai mươi mặt đều |
=> A đúng
+ Hình chóp tam giác đều là hình tứ diện đều → D đúng
+ Hình hộp chữ nhật có diện tích các mặt bằng nhau là khối lập phương → B đúng
+ Trọng tâm các mặt của hình tứ diện đều không thể là các đỉnh của một hình tứ diện đều → C sai.
Lời giải
Chọn A.
Lời giải
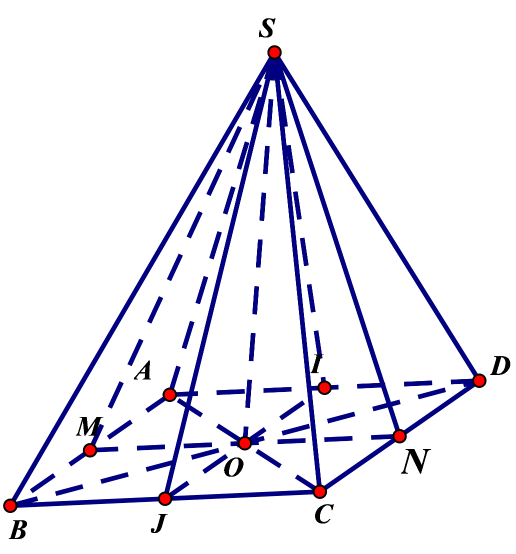
Hình chóp tứ giác đều có 4 mặt phẳng đối xứng đó là:
(SAC), (SBD), (SMN), (SIJ), với M, N, I, J lần lượt là trung điểm của AB, CD, DA, BC.
Chọn D.
Lời giải
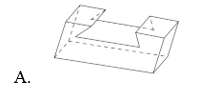
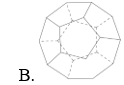
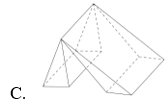
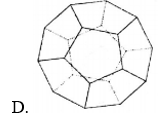
Chọn C.
Hình đa diện phải thỏa mãn 2 điều kiện:
+) Hai đa giác bất kì hoặc không có điểm chung, hoặc có 1 đỉnh chung hoặc có 1 cạnh chung.
+) Mỗi cạnh của một đa giác là cạnh chung của đúng 2 đa giác.
Hình C không thỏa mãn điều kiện thứ 2.
Lời giải
Chọn C.
Hình đa diện phải thỏa mãn 2 điều kiện:
+) Hai đa giác bất kì hoặc không có điểm chung, hoặc có 1 đỉnh chung hoặc có 1 cạnh chung.
+) Mỗi cạnh của một đa giác là cạnh chung của đúng 2 đa giác.
Hình C không thỏa mãn điều kiện thứ 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Khối chóp
B. Khối tứ diện
C. Khối hộp
D. Khối lăng trụ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.