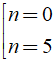Bài tập Đa giác. Đa giác đều (có lời giải chi tiết)
43 người thi tuần này 4.6 4.2 K lượt thi 10 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 10 (có đáp án)
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 8 (có đáp án)
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 1
Danh sách câu hỏi:
Câu 1/10
A. Hình vuông là đa giác đều.
B. Tổng các góc của đa giác lồi 8 cạnh là .
C. Hình thoi là đa giác đều.
D. Số đo góc của hình bát giác đều là
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta cần nhớ định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
+ Hình vuông là hình có 4 cạnh bằng nhau và 4 góc bằng nhau
⇒ Hình vuông là đa giác đều.
⇒ Đáp án A đúng.
+ Hình thoi là hình có 4 cạnh bằng nhau nhưng 4 góc không bằng nhau.
⇒ Hình thoi không phải là đa giác đều.
⇒ Đáp án C sai.
+ Tổng số đo các góc của đa giác n cạnh là
Khi đó tổng các góc của đa giác lồi 8 cạnh là
⇒ Đáp án B đúng.
+ Số đo của một góc của đa giác đều n cạnh là
Khi đó số đo của hình bát giác đều là
⇒ Đáp án D sai.
Đáp án C, D
Câu 2/10
A. 12.
B. 13.
C. 14.
D. Kết quả khác.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2.
Khi đó số đường chéo của đa giác 7 cạnh là (7( 7 - 3 ))/2 = 14 (đường chéo)
Chọn đáp án C.
Câu 3/10
A. 5.
B. 6.
C. 4.
D. 7.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )
Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n
⇔ 
So sánh điều kiện ta có n = 5 thỏa mãn.
Chọn A
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Tổng số đo các góc của đa giác n cạnh là
Do đó, Tổng số đo các góc của đa giác 12 cạnh là
Chọn đáp án A
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Số đường chéo xuất phát từ 1 đỉnh của đa giác n cạnh là n – 3
Do đó, Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là: 20 – 3 = 17
Chọn đáp án C
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Số đường chéo của đa giác n cạnh là:
Do đó số đường chéo của đa giác 10 cạnh là:
Chọn đáp án B.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8/10
A. n = 9
B. n = 8
C. n = 7
D. n = 10
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9/10
A. 45cm
B. 50cm
C. 60cm
D. 55cm
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 4/10 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập