200 câu trắc nghiệm Hàm số mũ và Logarit cơ bản (P3)

15 người thi tuần này 4.9 21.1 K lượt thi 30 câu hỏi 30 phút

🔥 Đề thi HOT:

2067 người thi tuần này

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)

80.9 K lượt thi 304 câu hỏi

1497 người thi tuần này

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

75.7 K lượt thi 126 câu hỏi

1087 người thi tuần này

20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)

13.6 K lượt thi 20 câu hỏi

1025 người thi tuần này

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

16.5 K lượt thi 20 câu hỏi

1006 người thi tuần này

124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)

15.4 K lượt thi 25 câu hỏi

976 người thi tuần này

62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)

14.9 K lượt thi 19 câu hỏi

959 người thi tuần này

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

13.1 K lượt thi 15 câu hỏi

929 người thi tuần này

7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)

12.4 K lượt thi 7 câu hỏi

Nội dung liên quan:

28 câu trắc nghiệm: Lũy thừa có đáp án

lượt thi

1 đề

25 câu Trắc nghiệm Lũy thừa có đáp án (Nhận biết)

lượt thi

1 đề

20 câu Trắc nghiệm Lũy thừa có đáp án (Thông hiểu)

lượt thi

1 đề

10 câu Trắc nghiệm Lũy thừa có đáp án (Vận dụng)

lượt thi

1 đề

68 câu Trắc nghiệm Lũy thừa có đáp án

lượt thi

1 đề

30 câu trắc nghiệm: Hàm số lũy thừa có đáp án

lượt thi

1 đề

15 câu Trắc nghiệm Hàm số lũy thừa có đáp án (Nhận biết)

lượt thi

1 đề

15 câu Trắc nghiệm Hàm số lũy thừa có đáp án (Thông hiểu)

lượt thi

1 đề

15 câu Trắc nghiệm Hàm số lũy thừa có đáp án (Vận dụng)

lượt thi

1 đề

32 câu Trắc nghiệm Hàm số lũy thừa có đáp án

lượt thi

1 đề

Danh sách câu hỏi:

Câu 1

Với giá trị nào của x thì biểu thức $A = \log_{\frac{1}{2}} \frac{x - 1}{3 + x}$ xác định?

A.-3≤ x≤ 1.

D. .-3< x < 1.

Lời giải

Biểu thức có nghĩa khi

Chọn B.

Câu 2

Với giá trị nào của x thì biểu thức: f( x) = log₆( 2x- x²) xác định?

A.0<x< 2.

B. x> 2.

C.-1< x< 1.

D.x< 3.

Lời giải

Biểu thức có nghĩa khi 2x- x²> 0 hay 0< x< 2

Chọn A.

Câu 3

Với giá trị nào của x thì biểu thức: f(x) = log₅( x³-x²-2x) xác định?

A. 0<x < 1.

B x> 1

Lời giải

Biểu thức có nghĩa khi: x³- x²-2x> 0 hay x( x²-x-2) > 0

Cách 1: Ta có bảng xét dấu sau:

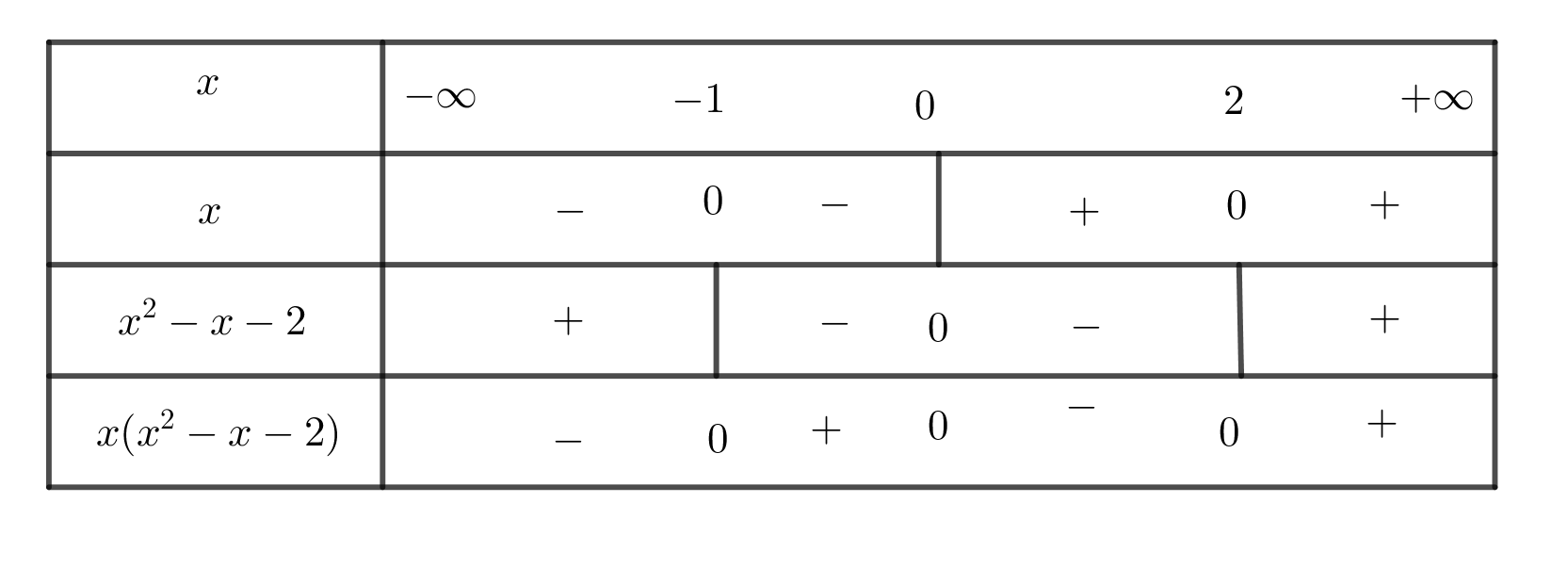
Suy ra: -1 < x < 0 hoặc x > 2

Vậy để biểu thức có nghĩa thì $x \in (- 1; 0) \cup (2; + \infty)$

Cách 2: sử dụng máy tính giải bất phương trình bậc 3.

Chọn C.

Câu 4

Điều kiện xác định của biểu thức $T = l o g \sqrt{(x^{2} - 4) (x^{2} - 6 x + 9)}$ là

B. x>3

Lời giải

+ Biểu thức có nghĩa khi ( x²- 4)( x²-6x+ 9) >0

Hay ( x²-4) ( x-3)²> 0

Ta có bảng xét dấu sau:

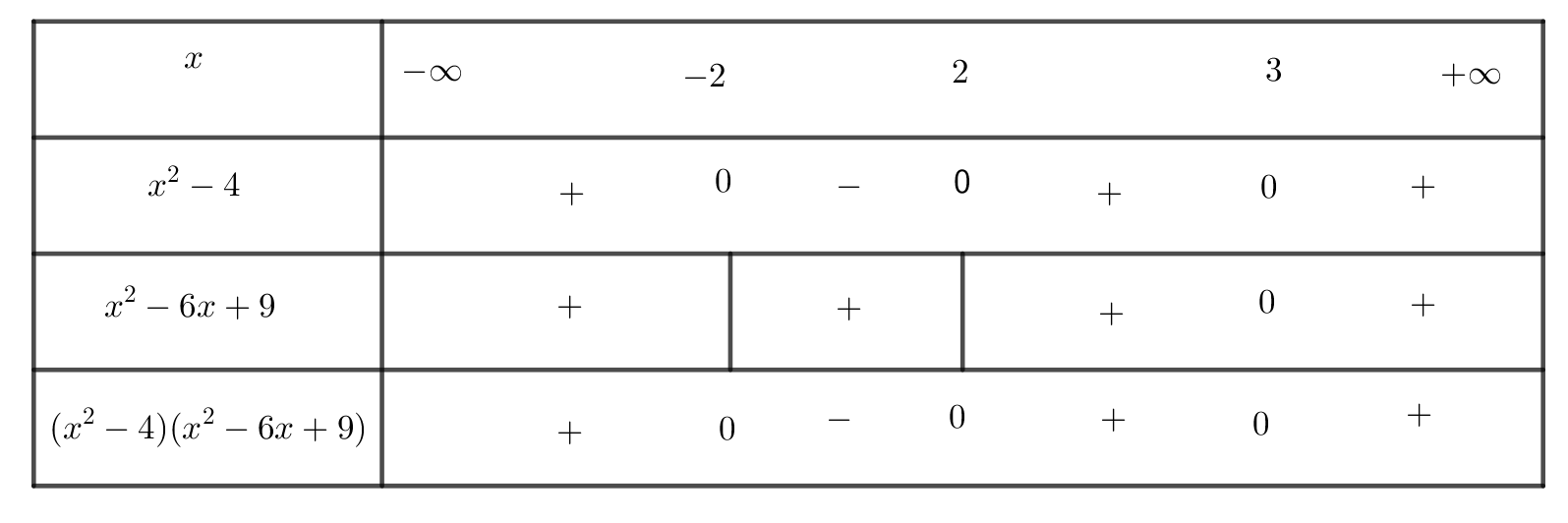
Suy ra biểu thức có nghĩa khi $x \in (- \infty; - 2) \cup (2; 3) \cup (3; + \infty)$

Chọn D.

Câu 5

Cho $\log_{2} x = 2 \log_{2} \sqrt[3]{a^{2}} + 3 \log_{2} \frac{1}{b^{2} \sqrt{b}} (a; b > 0)$ Khi đó:

D. x= ab

Lời giải

Ta có:

$\log_{2} x = 2 \log_{2} \sqrt[3]{a^{2}} + 3 \log_{2} \frac{1}{b^{2} \sqrt{b}} (a; b > 0), x > 0 \Leftrightarrow \log_{2} x = \log_{2} a^{\frac{4}{3}} + \log_{2} b^{- \frac{15}{2}} \Leftrightarrow \log_{2} x = \log_{2} a^{\frac{4}{3}} . b^{- \frac{15}{2}} \Leftrightarrow \log_{2} x = \log_{2} a^{\frac{4}{3}} . b^{- \frac{15}{2}} \Leftrightarrow x = a^{\frac{4}{3}} . b^{- \frac{15}{2}}$

Do đó $x = a^{\frac{4}{3}} . b^{\frac{- 15}{2}}$

Chọn B

Câu 6

Cho log_ax= m và log_abx= n ( a; b> 0) . Khi đó log_bx bằng

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử