Thi Online 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số
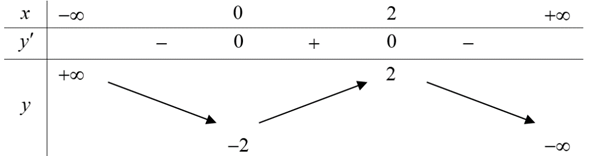
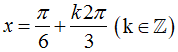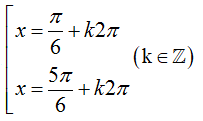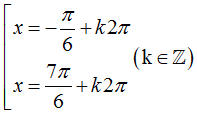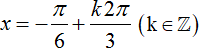250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1)
-
45387 lượt thi
-
30 câu hỏi
-
30 phút
Câu 2:
Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
(I) ; y = -x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
Chọn B.
Hàm số (I): 
, ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
Hàm số (II): y’ = -4x3 + 2x. y' = 0 <=> - 4x3 + 2x = 0 <=>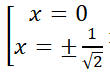 
nên hàm số không đồng biến trên khoảng xác định của nó.
Hàm số (III): y’ = 3x2 – 3.
y’ = 0 <=> 3x2 – 3 = 0 <=> x = ±1 nên hàm số không đồng biến trên khoảng xác định của nó.
Câu 3:
Cho hàm số
(m khác 1)
Chọn câu trả lời đúng
Chọn C.
Ta có:
Khi đó với m > 1 thì y’ > 0, ∀x ≠ 1.
Do đó hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1
Câu 5:
Hàm số nào sau đây nghịch biến trên R.
+) Xét hàm số: y = -x3 + 2x2 – x – 1
\( \Rightarrow y' = - 3{x^2} + 4x - 1 = \left( {x - 1} \right)\left( { - 3x + 1} \right)\)
+) Xét hàm số: \[y{\rm{ }} = {\rm{ }}\frac{1}{3}{x^3}--{\rm{ }}{x^2} + {\rm{ }}3x{\rm{ }} + {\rm{ }}1\]
\( \Rightarrow y' = {x^2} - 2x + 3 = {\left( {x - 1} \right)^2} + 2 > 0\forall x \in \mathbb{R}\)
Suy ra hàm số luôn đồng biến trên \(\mathbb{R}\)
+) Xét hàm số: \[y{\rm{ }} = {\rm{ }} - \frac{1}{3}{x^3}{\rm{ + }}{x^2} - x{\rm{ }}\]
\[ \Rightarrow y' = - {x^2}{\rm{ + 2}}x - 1 = - {\left( {x - 1} \right)^2} \le 0,\forall x \in \mathbb{R}\]
Suy ra hàm số luôn nghịch biến trên \(\mathbb{R}\)
+) Xét hàm số y = - x3 + 3x + 1
\( \Rightarrow y' = - 3{x^2} + 3 = - 3\left( {x - 1} \right)\left( {x + 1} \right)\)
Chọn C
Bài thi liên quan
Có thể bạn quan tâm
Các bài thi hot trong chương
Đánh giá trung bình
83%
17%
0%
0%
0%
Bình luận
Lê Dũng
10:19 - 17/07/2019
Ad ơi e chọn đáp án xong câu hỏi nhưng ấn vô phần "Câu hỏi tiếp theo không được ạ"
trogiangvietjack
22:18 - 17/03/2020
Có thể do lỗi hoặc do mạng
Lê Trọng Tuấn Vũ
14:01 - 07/04/2020
Đề hay lắm ad ak
Duc
20:46 - 14/06/2020
Câu 10 P1 tick B báo sai, nhưng lời giải lại ra B
Duc
20:50 - 14/06/2020
Câu 16 P1 đề không cho hàm số
Đào Thu Loan
08:59 - 07/07/2020
Ơ sao chọn B đúng nhưng lại hiện C đúng
Nguyễn Xuân Thắng
21:15 - 24/11/2020
câu 10 sai đáp án rồi admin
Huy Thảo
03:18 - 28/05/2021
câu 10 em chọn B sai nhưng lời giải ở dưới nó ghi B đúng
Huy Thảo
03:34 - 28/05/2021
câu 21 đáp án B sai mà lời giải ở dưới ghi B đúng
Kiều My
19:47 - 16/11/2022
21 b mà chừi ưiiiiiiiiiiiii
Nhận xét
3 năm trước
Trường Giang
2 năm trước
Muon Lo
2 năm trước
Đức Nguyễn
2 năm trước
Đoàn Thị Linh Hương
1 năm trước
chibi trang
1 năm trước
Quỳnh Tân