Dạng 4. Bài tập tự luyện số 1 có đáp án
24 người thi tuần này 4.6 5.2 K lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bài tập Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều lớp 8 (có lời giải)
Bài tập Tính diện tích xung quanh và thể tích của hình chóp tam giác đều lớp 8 (có lời giải)
Bài tập Các bài toán thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng lớp 8 (có lời giải)
Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore lớp 8 (có lời giải)
Bài tập Chứng minh các tính chất hình học lớp 8 (có lời giải)
Bài tập Tính độ dài cạnh trong tam giác vuông bằng cách sử dụng định lí Pythagore lớp 8 (có lời giải)
Danh sách câu hỏi:
Lời giải
Hình vuông có các tính chất sau về đường chéo.
a) Hai đường chéo cắt nhau tại trung điểm của mỗi đường (có ở hình bình hành).
b) Hai đường chéo bằng nhau (có ở hình chữ nhật).
c) Hai đường chéo vuông góc với nhau (có ở hình thoi).
d) Hai đường chéo là các đường phân giác của các góc của hình vuông (có ở hình thoi).
Lời giải
Lời giải
Lời giải
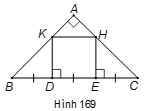
Tứ giác KHED là hình vuông.
Giải thích: Tam giác vuông BDK có nên là tam giác cân,
do đó BD = DK. Chứng minh tương tự, HE = EC.
Vì BD = DE = EC theo giả thiết, nên:
KD = DE = EH.
Tứ giác KHED có nên là hình bình hành.
Hình bình hành này lại có nên nó là hình chữ nhật.
Hình chữ nhật này lại có KD = DE nên nó là hình vuông.
Lời giải
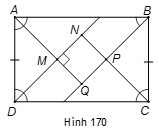
Vì có nên vuông cân tại 
.
Suy ra và ND = NC (1).
Chứng minh tương tự, . Tứ giác MNPQ có ba góc
vuông nên là hình chữ nhật.
(g-c-g) => MD = PC (2).
Trừ theo vế đẳng thức (1) cho đẳng thức (2) ta được NM = NP.
Như vậy hình chữ nhật MNPQ có hai cạnh kề bằng nhau nên là hình vuông.
Lời giải
Chứng minh bốn tam giác vuông bằng nhau để suy ra EG = GI = IC và .
Sau đó chứng minh .
Nhắn tin Zalo
Hỏi bài tập