Dạng 5: Bài tập tự luyện có đáp án

22 người thi tuần này 4.6 3.5 K lượt thi 11 câu hỏi 45 phút

🔥 Học sinh cũng đã học

505 người thi tuần này

Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 2

1.4 K lượt thi 11 câu hỏi

404 người thi tuần này

Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 1

1.3 K lượt thi 11 câu hỏi

244 người thi tuần này

Bài tập ôn tập Toán 8 Chương 10 (có đáp án)

488 lượt thi 50 câu hỏi

106 người thi tuần này

Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 2

594 lượt thi 11 câu hỏi

169 người thi tuần này

Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 1

657 lượt thi 11 câu hỏi

148 người thi tuần này

Bài tập ôn tập Toán 8 Chương 8 (có đáp án)

405 lượt thi 50 câu hỏi

94 người thi tuần này

Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 2

552 lượt thi 11 câu hỏi

158 người thi tuần này

Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 1

616 lượt thi 11 câu hỏi

Danh sách câu hỏi:

Câu 1/11

Cho hình vẽ trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua C.

Xem đáp án

Lời giải

Cho hình vẽ trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua C. (ảnh 2)

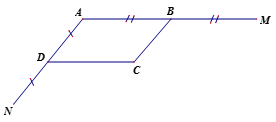
Ta có AB = CD (ABCD là hình bình hành)

AB = BM (gt)

=> CD= BM

Ta có AB // CD (ABCD là hình bình hành)

=> BM// CD

Xét tứ giác BDCM có

CD=BM (cmt)

CD//BM (cmt)

=> Tứ giác BDCM là hình bình hành

=> BD//CM; BD=CM (1)

Chứng minh tương tự ta có BD//NC; BD= NC (2)

Từ (1) và (2) và theo tiên đề Ơclit suy ra N, C, M thẳng hàng và CM = CN

Do đó N đối xứng với M qua C.

Câu 2/11

Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua điểm A.

Xem đáp án

Lời giải

Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với C qua N. (ảnh 1)

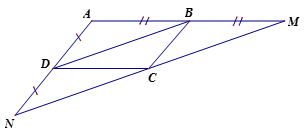
Xét tứ giác ABCD có

AM = MC (BM là trung tuyến của tam giác ABC)

BM = MD (D đối xứng với B qua M)

=> Tứ giác ABCD là hình bình hành

=> AD//BC; AD = BC (1)

Xét tứ giác ACBE có

AN = NB (CN là trung tuyến của tam giác ABC)

NE = NC (E đối xứng với C qua N)

=> Tứ giác ACBE là hình bình hành

=> AE//BC; AE = BC (2)

Từ (1) và (2) Theo tiên đề Ơclit suy ra A, D, E thẳng hàng và AD = AE

Do đó D đối xứng với E qua A

Câu 3/11

Cho tam giác ABC vuông tại A, điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, gọi F là điểm đối xứng với D qua AC. Chứng minh rằng các điểm E và F đối xứng nhau qua điểm A.

Xem đáp án

Lời giải

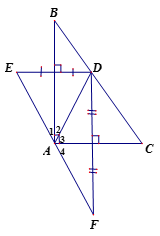
Cho tam giác ABC vuông tại A, điểm D thuộc cạnh BC. Gọi E là điểm đối xứng với D qua AB, gọi F là điểm đối xứng với D qua AC. (ảnh 1)

Ta có E đối xứng với D qua AB

=> AB là đường trung trực của ED

=> $△$ AE= AD (1)

=> ADE cân tại A

=> AB là đường phân giác

=> $\hat{A_{1}} = \hat{A_{2}}$ (2)

Ta có F đối xứng với D qua AC

=> AC là đường trung trực của FD

=> AF= AD (3)

=> $△$ ADF cân tại A

=> AC là đường phân giác

=> $\hat{A_{3}} = \hat{A_{4}}$ (4)

Từ (1) và (3) => AE= AF (5)

Ta có $\hat{E A F} = \hat{A_{1}} + \hat{A_{2}} + \hat{A_{3}} + \hat{A_{4}} (6)$

Từ (2)(4) và (6) suy ra

$\begin{array}{l} \hat{E A F} = \hat{A_{2}} + \hat{A_{2}} + \hat{A_{3}} + \hat{A_{3}} \\ = 2 (\hat{A_{2}} + \hat{A_{3}}) \\ = 2 \hat{B A C} \\ = {2.90}^{0} \\ = 180^{0} \end{array}$

=> E, A, E thẳng hàng (7)

Từ (5) và (7) suy ra E đối xứng với F qua A

Câu 4/11

Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt hai cạnh đối AD, BC ở E, F. Chứng minh rằng các điểm E và F đối xứng nhau qua điểm O.

Xem đáp án

Lời giải

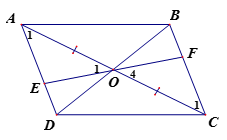
Ta có ABCD là hình bình hành

=> AD//BC

=> $\hat{A_{1}} = \hat{C_{1}}$ (2 góc so le trong)

O là giao điểm của 2 đường chéo

=> OA = OC

Xét $△$ AOE và $△$ COF có

$\hat{A_{1}} = \hat{C_{1}}$ (cmt)

OA = OC (cmt)

OA = OC (2 góc đối đỉnh)

=> $△$ AOE = $△$ COF (g.c.g)

=> OE = OF

Do đó E đối xứng với F qua O

Câu 5/11

Cho tam giác ABC, D là một điểm trên BC, Qua D vẽ DE //AB (E thuộc AC) vẽ DF//AC (F thuộc AB). Gọi I là trung điểm của AD. Chứng minh rằng E đối xứng với F qua điểm I.

Xem đáp án

Lời giải

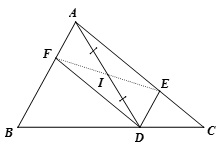
Cho tam giác ABC, D là một điểm trên BC, Qua D vẽ DE //AB (E thuộc AC) vẽ DF//AC (F thuộc AB). (ảnh 1)

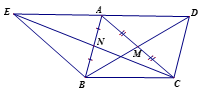
Xét tứ giác AEDF có

AF//DE (DE//AB)

AE//DF (DF//AC)

=> Tứ giác AEDF là hình bình hành

Có I là trung điểm của đường chéo AD

=> I là trung điểm của đường chéo EF

Do đó E đối xứng với F qua điểm I.

Câu 6/11

Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là điểm bất kỳ nằm trong tam giác ABC. Vẽ M đối xứng với O qua D, vẽ N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.

Xem đáp án

Lời giải

Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là điểm bất kỳ nằm trong tam giác ABC (ảnh 1)

Xét tứ giác AOCN có

AE = EC (gt)

OE = EN (N đối xứng với O qua E)

=> Tứ giác AOCN là hình bình hành

AO // NC; AO = NC (1)

Xét tứ giác AOBM có

AD = DB (gt)

OD = DM (N đối xứng với O qua E)

=> Tứ giác AOBM là hình bình hành

=> AO // MB; AO = MB (1)

Từ (1) và (2) => BM // CN; BM = CN

Xét tứ giác MNCB có

BM // CN (cmt)

BM = CN (cmt)

Do đó tứ giác MNCB là hình bình hành

Câu 7/11