Trắc nghiệm Toán 12 Bài 2: Mặt cầu có đáp án (Mới nhất)

Thi Online Trắc nghiệm Toán 12 Bài 2: Mặt cầu có đáp án (Mới nhất)

Đề số 1

Trắc nghiệm Toán 12 Bài 2: Mặt cầu có đáp án (Mới nhất)

314 lượt thi
109 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Cho đường tròn (C) đường kính AB và đường thẳng $Δ$ . Để hình tròn xoay sinh bởi (C) khi quay quanh $Δ$ là một mặt cầu thì cần có thêm điều kiện nào sau đây:

(I) Đường kính AB thuộc $Δ$ .

(II) $Δ$ cố định và đường kính AB thuộc $Δ$ .

(III) $Δ$ cố định và hai điểm A, B cố định trên $Δ$ .

A. Chỉ (I).

B. Chỉ (II).

C. Chỉ (III).

D. Không cần thêm điều kiện nào.

Xem đáp án

Chọn C

Câu 2:

Cho mặt cầu (S) tâm O, bán kính R và mặt phẳng (P) có khoảng cách đến O bằng R. Một điểm M tùy ý thuộc (S). Đường thẳng OM cắt (P) tại N. Hình chiếu của O trên (P) là I. Mệnh đề nào sau đây đúng?

A. NI tiếp xúc với (S)

O N = R \sqrt{2} \Leftrightarrow I N = R .

C. Cả A và B đều sai.

D. Cả A và B đều đúng.

Xem đáp án

Chọn D

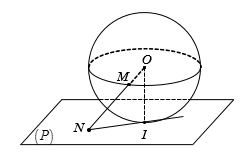
Vì I là hình chiếu của O trên (P) nên d[O, (P)] = OI mà d[O, (P)] = R nên I là tiếp điểm của (P) và (S).

Đường thẳng OM cắt (P) tại N nên IN vuông góc với OI tại I. Suy ra IN tiếp xúc với (S).

Tam giác OIN vuông tại I nên $O N = R \sqrt{2} \Leftrightarrow I N = R$

Câu 3:

Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:

A. $R$

B. $\frac{R}{2}$

C. $R \sqrt{2}$

D. $R \sqrt{3}$

Xem đáp án

Chọn D

Vì AB tiếp xúc với (S) tại B nên $A B ⊥ O B$

Suy ra $A B = \sqrt{O A^{2} - O B^{2}} = \sqrt{4 R^{2} - R^{2}} = R \sqrt{3} .$

Câu 4:

Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một cát tuyến cắt (S) tại B và C sao cho $B C = R \sqrt{3}$ . Khi đó khoảng cách từ O đến BC bằng:

A. $R$

B. $\frac{R}{2}$

C. $R \sqrt{2}$

D. $R \sqrt{3}$

Xem đáp án

Chọn B

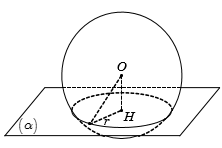
Gọi H là hình chiếu của O lên BC.

Ta có OB = OC = R, suy ra H là trung điểm của BC nên $H C = \frac{C D}{2} = \frac{R \sqrt{3}}{2}$ .

Suy ra

O H = \sqrt{O C^{2} - H C^{2}} = \frac{R}{2} .

Câu 5:

Cho mặt cầu S(O;R) và mặt phẳng $(α)$ . Biết khoảng cách từ O đến $(α)$ bằng $\frac{R}{2}$ . Khi đó thiết diện tạo bởi mặt phẳng $(α)$ với S(O;R) là một đường tròn có đường kính bằng:

A. $R$

B. $R \sqrt{3}$

C. $\frac{R}{2}$

D. $\frac{R \sqrt{3}}{2}$

Xem đáp án

Chọn B

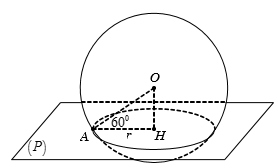
Gọi H là hình chiếu của xuống $(α)$

Ta có $d [O, (α)] = O H = \frac{R}{2} < R$ nên $(α)$ cắt S(O;R) theo đường tròn C(H;r).

Bán kính đường tròn $C (H; r)$ là $r = \sqrt{R^{2} - O H^{2}} = \frac{R \sqrt{3}}{2} .$

Suy ra đường kính bằng

R \sqrt{3} .

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Các bài thi hot trong chương:

32 câu trắc nghiệm: Mặt cầu có đáp án

( 2.7 K lượt thi )

Trắc nghiệm Mặt cầu có đáp án (Nhận biết)

( 1.7 K lượt thi )

Trắc nghiệm Mặt cầu có đáp án (Thông hiểu)

( 1.6 K lượt thi )

Trắc nghiệm Mặt cầu có đáp án (Vận dụng)

( 1.6 K lượt thi )

Trắc nghiệm Mặt cầu có đáp án

( 1.5 K lượt thi )

52 câu trắc nghiệm: Khái niệm về mặt tròn xoay có đáp án

( 3.5 K lượt thi )

20 câu trắc nghiệm: Ôn tập chương 2 Hình học 12 có đáp án

( 2.4 K lượt thi )

Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Vận dụng)

( 2.2 K lượt thi )

Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án

( 2.1 K lượt thi )

Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Nhận biết)

( 2 K lượt thi )

Đánh giá trung bình

Thi Online Trắc nghiệm Toán 12 Bài 2: Mặt cầu có đáp án (Mới nhất)