Thi Online Đề thi Giữa kì 1 Toán 8 có đáp án
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 1)
-
3903 lượt thi
-
5 câu hỏi
-
30 phút
Câu 1:
Phân tích các đa thức sau thành nhân tử:
1) A = x2– 5x + 4;
2) B = 9x2+ 4y2– 12xy – 4;
Hướng dẫn giải
1) A = x2– 5x + 4
= x2– 4x – x + 4
= x(x – 4) – (x – 4)
= (x – 4)(x – 1)
2) B = 9x2+ 4y2– 12xy – 4
= ((3x2) – 2 . 3x . (2y)2) – 4
= (3x – 2y)2– 4
= (3x – 2y – 2)(3x – 2y + 2).
Câu 2:
Tìm x sao cho (x + 2)3+ (x – 2)3= 24x + 16.
Hướng dẫn giải
(x + 2)3+ (x – 2)3= 24x + 16
⇔ x3+ 6x2+ 12x +8 + x3– 6x2+ 12x – 8 = 24x + 16
⇔ 2x3+ 24x = 24x + 16
⇔ 2x3= 16
⇔ x3= 8
⇔ x = 2
Vậy x = 2.
Câu 3:
Cho a, b, c là các số thực thỏa mãn a2+ b2+ c2= ab + bc + ca, chứng minh rằng a = b = c.
Hướng dẫn giải
a2+ b2+ c2= ab + bc + ca
⇔ 2(a² + b² + c²) = 2ab+ 2bc + 2ca
⇔ 2a² + 2b² + 2c² = 2ab + 2bc + 2ca
⇔ (a² – 2ab + b²) + (b² – 2bc + c²) + (a² – 2ac + c²) =0
⇔ (a – b)² + (b – c)² + (a – c)² = 0
Vì (a – b)² ≥ 0 với ∀ a, b
Vì (b – c)² ≥ 0 với ∀ c, b
Vì (a – c)² ≥ 0 với ∀ a, c
⇒ (a – b)² + (b – c)² + (a – c)² ≥ 0
Để (a – b)² + (b – c)² + (a – c)² = 0
\( \Rightarrow \left[ \begin{array}{l}a - b = 0\\b - c = 0\\c - a = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}a = b\\b = c\\c = a\end{array} \right.\)
⇔ a = b = c (đpcm).
Câu 4:
Cho tam giác ABC có M, D lần lượt là trung điểm của BC, AC, P là hình chiếu vuông góc của B lên trung trực của AC. Gọi E là giao điểm của MP với AB, F là giao điểm của EM với AC
1 Chứng minh: BFCP là hình bình hình.
2) Tia DM cắt tia BP tại Q. Chứng minh: DPQF là hình chữ nhật.
3) Chứng minh: Tam giác EBP cân
Hướng dẫn giải
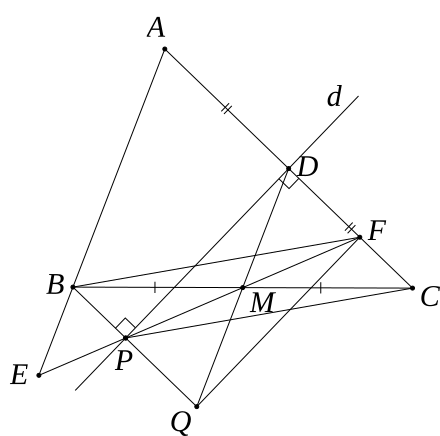
1) Ta có:
BP ⊥ d (gt)
CF ⊥ d (do d là đường trung trực AC)
⇒ BP // CF
Xét ΔBMP và ΔCMF có:
\(\widehat {BMP} = \widehat {FMC}\) (đối đỉnh)
BM = MC (gt)
\(\widehat {PBM} = \widehat {MCF}\) (so le trong)
⇒ ΔBMP = ΔCMF (g.c.g)
⇒ PM = MF
Xét tứ giác BPCF có:
PM = MF (cmt)
BM = MC (do M là trung điểm BC)
⇒ Tứ giác BPCF là hình bình hành (2 đường chéo cắt nhau tại trung điểm của mỗi đường)
2) Xét ΔPMQ và ΔFMD có:
\(\widehat {PMQ} = \widehat {FMD}\)(cmt)
PM = MF (cmt)
\(\widehat {MPQ} = \widehat {MFD}\) (do BP // CF, so le trong)
⇒ ΔPMQ = ΔFMD (g.c.g)
⇒ QM = MD
⇒ M là trung điểm QD
Xét tứ giác DPQF có
M là trung điểm của QD (cmt)
M là trung điểm của PF (cmt)
⇒Tứ giác DPQF là hình bình hành
Lại có: PD ⊥ DF (do d là đường trung trực của AC mà PD thuộc d và DF thuộc AC)
Hình bình hành DPQF có một góc vuông
⇒ DPQF là hình chữ nhật
3) Ta có: DPQF là hình chữ nhật
⇒ PF = QD (2 đường chéo của hình chữ nhật) và PM = QM (=1/2 PF = 1/2 QD)
Xét ΔPMQ có PM = QM ⇒ ΔPMQ cân tại M
\( \Rightarrow \widehat {MPQ} = \widehat {MQP}\) (1)
Tứ giác BPCF là hình bình hành ⇒ BP = CF
Tứ giác DPQF là hình chữ nhật ⇒ PQ = DF
Suy ra BP + PQ = CF + DF ⇒ BQ = DC
Mà DC = AD (vì D là trung điểm của AC)
Xét tứ giác ADQB có AD = BQ và AD//BQ
⇒ ADQB là hình bình hành
⇒ AB // QD
\( \Rightarrow \widehat {EBP} = \widehat {MQP}\) (so le trong (2)
Ta có : \(\widehat {BPE} = \widehat {MPQ}\) (đối đỉnh) (3)
Từ (1), (2), (3) \( \Rightarrow \widehat {BPE} = \widehat {EBP}\)
Xét ΔEBP có: \(\widehat {BPE} = \widehat {EBP}\) (cmt)
⇒ ΔEBP cân tại E
Câu 5:
Với các số thực x, y thỏa mãn x + y = 1. Tìm giá trị nhỏ nhất của biểu thức
A = x3+ y3+ 2xy.
Hướng dẫn giải
Ta có: x2+ 2xy + y2 = (x + y)2= 12= 1 (1)
A = x3+ y3+ 2xy
= (x + y)(x2– xy + y2) + 2xy
= x2– xy + y2+ 2xy
= x2+ xy + y2
Suy ra : 2A = 2x2+ 2xy + 2y2= (x + y)2+ x2+ y2= 1 + x2+ y2
Lại có: (x – y)2≥ 0
⇒ x2– 2xy + y2≥ 0 (2)
Từ (1) và (2)
⇒ (x2+ 2xy + y2) + (x2– 2xy + y2) ≥ 1
⇒ 2(x2+ y2) ≥ 1
\[ \Rightarrow {x^2} + {y^2} \ge \frac{1}{2}\]
\[ \Rightarrow {x^2} + {y^2} + 1 \ge \frac{3}{2}\]
\[ \Rightarrow 2A \ge \frac{3}{2}\]
\[ \Rightarrow A \ge \frac{3}{4}\]
Dấu “=” xảy ra \[ \Leftrightarrow x = y = \frac{1}{2}\]
Vậy với \[x = y = \frac{1}{2}\] thì giá trị nhỏ nhất của \[A \ge \frac{3}{4}\].
Bài thi liên quan:
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 2)
13 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 3)
5 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 4)
4 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 5)
6 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 6)
5 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 7)
17 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 8)
5 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 9)
13 câu hỏi 30 phút
Các bài thi hot trong chương:
( 7.6 K lượt thi )
( 5.5 K lượt thi )
( 7.4 K lượt thi )
( 4.1 K lượt thi )
( 5.4 K lượt thi )
( 10.1 K lượt thi )
( 9.9 K lượt thi )
( 8.3 K lượt thi )
( 8.1 K lượt thi )
( 7.7 K lượt thi )
Đánh giá trung bình
0%
0%
0%
0%
0%
Anh Truong
21:46 - 03/01/2023
câu 1
a) (x-1)(x-4)
b)(3x +2y-2)(3x+2y+2)