Thi Online Đề thi Giữa kì 1 Toán 8 có đáp án
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 5)
-
3889 lượt thi
-
6 câu hỏi
-
30 phút
Câu 1:
Cho hai biểu thức.
A = x2– x + 5 và B = (x – 1)(x + 2) – x(x – 2) – 3x
a) Tính giá trị biểu thức A khi x = 2;
b) Chứng tỏ B = – 2 với mọi giá trị của biến x;
c) Tìm giá trị nhỏ nhất của biểu thức C = A + B.
Hướng dẫn giải
a) Tại x = 2
⇒ A = 22– 2 + 5 = 7
Vậy tại x = 2 thì A = 7.
b) B = (x – 1)(x + 2) – x(x – 2) – 3x
= x2+ x – 2 – x2+ 2x – 3x
= – 2 (đpcm)
c) A + B = x2– x + 5 – 2
= x2– x + 3
\( = \left( {{x^2} - 2.\frac{1}{2}.x + \frac{1}{4}} \right) + \frac{{11}}{4}\)
\( = {\left( {x - \frac{1}{2}} \right)^2} + \frac{{11}}{4}\)
Mà \({\left( {x - \frac{1}{2}} \right)^2} \ge 0{\rm{ }}\forall x\)
\( \Rightarrow {\left( {x - \frac{1}{2}} \right)^2} + \frac{{11}}{4} \ge \frac{{11}}{4}\)
\( \Leftrightarrow C \ge \frac{{11}}{4}\)
Dấu bằng xảy ra khi \({\left( {x - \frac{1}{2}} \right)^2} = 0 \Leftrightarrow x = \frac{1}{2}\)
Vậy giá trị nhỏ nhất của C là \(\frac{{11}}{4}\) khi \(x = \frac{1}{2}\).
Câu 2:
Phân tích đa thức thành nhân tử:
a) x2– 8x;
b) x2– xy – 6x + 6y;
c) x2– 6x + 9 – y2;
d) x3+ y3+ 2x + 2y.
Hướng dẫn giải
a) x2– 8x = x(x – 8)
b) x2– xy – 6x + 6y
= x(x – 6) – y(x – 6)
= (x – 6)(x – y)
c) x2– 6x + 9 – y2
= (x2– 6x + 9) – y2
= (x – 3)2– y2
= (x – 3 – y)(x – 3 + y)
d) x3+ y3+ 2x + 2y
= (x3+ y3) + 2(x + y)
= (x + y)(x2– xy + y2) + 2(x + y)
= (x + y)(x2– xy + y2+ 2)
Câu 3:
Tìm các số thực x, biết:
a) (2x – 3)2– 49 = 0
b) 2x(x – 5) – 7(5 – x) = 0
c) x2– 3x – 10 = 0
Hướng dẫn giải
a) (2x – 3)2– 49 = 0
⇔ (2x – 3)2– 72= 0
⇔ (2x – 3 – 7)(2x – 3 + 7) = 0
⇔ (2x – 10)(2x + 4) = 0
\( \Leftrightarrow \left[ \begin{array}{l}2x - 10 = 0\\2x + 4 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = - 2\end{array} \right.\)
Vậy x = 5, x = - 2.
b) 2x(x – 5) – 7(5 – x) = 0
⇔ 2x(x – 5) + 7(x – 5) = 0
⇔ (x – 5)(2x + 7) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\2x + 7 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = - \frac{7}{2}\end{array} \right.\)
Vậy \(x = - \frac{7}{2}\), x = 5.
c) x2– 3x – 10 = 0
⇔ x2– 5x + 2x – 10 = 0
⇔ x(x – 5) + 2(x – 5) = 0
⇔ (x – 5)(x + 2) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x - 5 = 0\\x + 2 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = - 2\end{array} \right.\)
Vậy x = 5, x = – 2.
Câu 4:
Cho hình vẽ bên, biết AB//CD, AB = 5cm, CD = 7cm. Tính EG.
Hướng dẫn giải
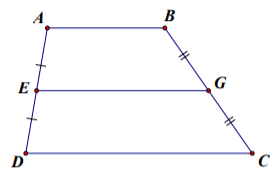
Tứ giác ABCD là hình thang (AB//CD)
Ta thấy EA = ED, GB = GC
⇒ EG là đường trunng bình của hình thang ABCD
\( \Rightarrow EG = \frac{{AB + CD}}{2} = \frac{{5 + 7}}{2} = 6\) (cm)
Câu 5:
Cho ∆ABC có E là trung điểm của AC. Qua E kẻ ED//AB (D ∈ BC);
EF//BC (F ∈ AB)
a) Chứng minh tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC.
b) Gọi H là điểm đối xứng của D qua F. CHứng minh rằng HB//AD.
c) Gọi I là trung điểm của HB; K là giao điểm của AD và EF. Chứng minh rằng I, K, E thẳng hàng.
d) ∆ABC cần thêm điều kiện gì để \(HF = \frac{{AB}}{2}\).
Hướng dẫn giải
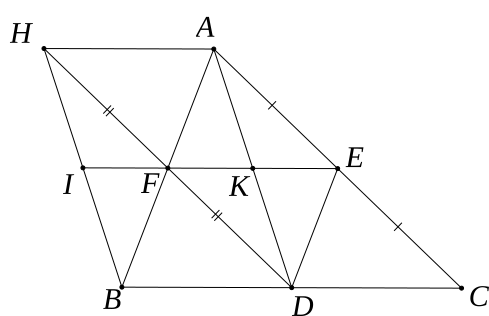
a)
Xét tứ giác BDEF cóEF // BD (vì EF//BC)
ED // FB (vì ED//AB)
Do đó tứ giác BDEF là hình bình hành (tứ giác có cặp cạnh đối song song)
Tam giác ABC có:
EA = EC (gt)
ED // AB (gt)
Do đó DB = DC hay D là trung điểm của đoạn thẳng BC.
b) Vì H đối xứng D qua F
⇒ F là trung điểm của HD (1)
Vì E là trung điểm của AC và EF//BC
⇒ F là trung điểm của AB (2)
Từ (1) và (2) ⇒ tứ giác HABD có hai đường chéo cắt nhau tại trung điểm mỗi đường.
⇒ AHBD là hình hình hành
⇒ HB//AD.
c) Xét tam giác HBD có:
I là trung điểm của HB
F trung điểm của HD
⇒ IF// BD (3)
Mà FE//BD (4)
⇒ I, F, E thẳng hàng.
⇒ I, K, E thẳng hàng.
d) Để \(HF = \frac{{AB}}{2}\) thì \(\frac{{HD}}{2} = \frac{{AB}}{2}\)
⇒ HD = AB
Hình bình hành AHBD có HD = AB
⇒ AHBD là hình chữ nhật
⇒ AD vuông góc với BC
Xét tam giác ABC có AD vừa là đường cao vừa là đường trung tuyến (D là trung điểm của BC)
⇒ ΔABC cân tại A.
Vậy ∆ABC cân tại A thì \(HF = \frac{{AB}}{2}\)
Bài thi liên quan:
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 1)
5 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 2)
13 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 3)
5 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 4)
4 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 6)
5 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 7)
17 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 8)
5 câu hỏi 30 phút
Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 9)
13 câu hỏi 30 phút
Các bài thi hot trong chương:
( 7.6 K lượt thi )
( 5.5 K lượt thi )
( 7.4 K lượt thi )
( 4.1 K lượt thi )
( 5.4 K lượt thi )
( 10.1 K lượt thi )
( 9.8 K lượt thi )
( 8.2 K lượt thi )
( 8.1 K lượt thi )
( 7.6 K lượt thi )
Đánh giá trung bình
0%
0%
0%
0%
0%