225 Bài tập Số phức ôn thi Đại học có lời giải (P8)
19 người thi tuần này 4.0 13.8 K lượt thi 24 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. Một đường thẳng.
B. Một đường Parabol.
C. Một đường tròn có bán kính bằng 2.
D. Một đường tròn có bán kính bằng 4.
Lời giải
Đáp án C
Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
Số phức z1 được biểu diễn bởi điểm A(1;-1).
Em có: |z - 1 + i| = 2 => MA = 2
Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: ![]()
Cách 2: Đặt ![]() . Số phức z được biểu diễn bởi điểm M(x;y).
. Số phức z được biểu diễn bởi điểm M(x;y).
Em có:
![]()
![]()
![]()
Vậ tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình: ![]()
Câu 2
A. -3 - 3
B. 3 + 3
C. 3 - 3
D. -3 + 3
Lời giải
Đáp án D
Đặt ![]() Số phức z được biểu diễn bởi điểm
Số phức z được biểu diễn bởi điểm ![]()
Đặt![]() Số phức z2 được biểu diễn bởi điểm
Số phức z2 được biểu diễn bởi điểm ![]()
Suy ra: |z1 - z2| = MN
Em có: ![]()
![]()
Vậy điểm M thuộc đường tròn ![]() có tâm là điểm I(5;1) bán kính R = 3
có tâm là điểm I(5;1) bán kính R = 3
Em có
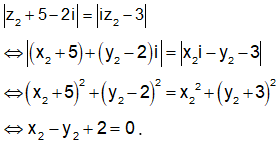
Vậy điểm N thuộc đường thẳng d: x - y + 2 = 0.
Dễ thấy đường thẳng d và đường tròn C không cắt nhau.
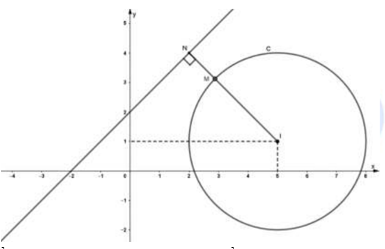
Áp dụng bất đẳng thức tam giác cho bộ ba điểm I, M, N em có:
![]()
![]()
Dấu “=” bằng xảy ra khi và chỉ khi I, M, N thẳng hàng và N là hình chiếu của I trên đường thẳng d.
Vậy ![]()
Câu 3
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Lời giải
Đáp án D
Đặt z = a + bi
![]()
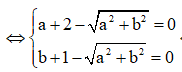
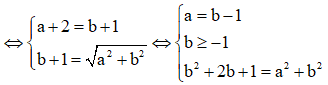
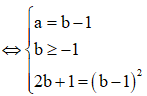
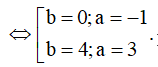
![]()
Câu 4
A. P = 10
B. P = 4
D. P = 6
D. P = 8
Lời giải
Đáp án A
Gọi M(x;y) là điểm biều diễn số phức z.
Từ giả thiết, ta có |z - 4 - 3i| = 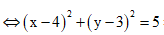
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R =
Khi đó P = MA + MB với A(-1;3), B(1;-1)
Ta có ![]()
Gọi E(0;1) là trung điểm của AB ![]()
Do đó ![]() mà
mà ![]() suy ra
suy ra ![]()
Với C là giao điểm của đường thẳng EI với đường tròn (C)
Vậy ![]() Dấu “=”xảy ra
Dấu “=”xảy ra 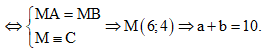
Câu 5
A. -i
B. -1
C. 2
D. -2i
Lời giải
Đáp án C
giả sử ![]()
The giả thiết, ta có
![]()
![]()
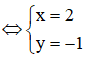
Suy ra ![]()
Ta có ![]()
![]()
Vậy chọn phần ảo là – 1
Câu 6
A. P = 5
B. P = -2
C. P = 3
D. P = 1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. M(3;-1)
B. M(3;1)
C. M(-3;1)
D. M(-3;-1)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. M + m = 63
B. M + m = 48
C. M + m = 50
D. M + m = 41
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. đường thẳng
B. đường tròn
C. parabol
D. hypebol
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A.
B. 3
C.
D. 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. 6
B. -3
C. 3
D. -6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. y = x + 1
B. y = -x + 1
C. y = -x - 1
D. y = x - 1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. || =
B. || =
C. || =
D. || =
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. đường tròn tâm là gốc tọa độ, bán kính bằng ||
B. đường tròn tâm là điểm biểu diễn số phức -, bán kính bằng
C. đường tròn tâm là gốc tọa độ, bán kính bằng
D. đường tròn tâm là điểm biểu diễn số phức bán kính bằng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. α là số thực, β là số thực.
B. α là số ảo, β là số thực.
C. α là số thực, β là số ảo.
D. α là số ảo, β là số ảo.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. 5.
B. 1.
C.
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. cân tại O.
B. Vuông cân tại O.
C. đều.
D. Vuông tại O.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. 2M - m =
B. 2M - m =
C. 2M - m = 10
D. 2M - m = 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.