Bài tập Hình học không gian OXYZ cơ bản, nâng cao có lời giải (P5)
32 người thi tuần này 4.6 18.3 K lượt thi 30 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
Đáp án B
Lời giải
Đáp án C
Gợi A’, B’ C’ hình chiếu của A lên Ox, Oy, Oz. Ta có:
A'(5;0;0), B'(0;4;0), C(0;0;3) => PT :
Câu 3
A. 1
B. 4
C. 5
D. không tồn tại
Lời giải
Đáp án C
, , => ABCD là hình bình hành
là hình chóp đáy hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên
+ Mặt phẳng qua 4 trung điểm lần lượt là AD, EC, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt là EC, EB, DC, AB
+ Mặt phẳng qua 4 trung điểm lần lượt là EA, EB, AD, BC
+ Mặt phẳng qua 4 trung điểm lần lượt là EA, ED, AB, DC
Câu 4
A. bc = 2( b + c )
B.
C. b + c = bc
D. bc = b - c
Lời giải
Đáp án A
![]()
![]()
Theo giả thiết 4 điểm M, N, B, C đồng phẳng nên
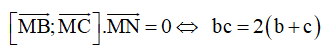
Lời giải
Đáp án B
![]()
![]()
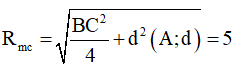
vậy phương trình mặt cầu cần tìm là
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. S(0;0;3)
B. R(1;0;0)
C. Q(0;2;0)
D. P(1;0;3)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. m = 1
B. Không tồn tại m
C. m = -2
D. m = 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. x + z = 0
B. y + z +1 = 0
C. y = 0
D. x + y + z = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. M(3;3;-3)
B. M(-3;-3;3)
C. M(3;-3;3)
D. M(-3;3;3)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. 4x + 2y - z + 4 = 0
B. 4x + 2y + z - 4 = 0
C. 4x - 2y - z + 4 = 0
D. 4x - 2y + z + 4 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. I(2;0;-1)
B. I(0;0;-1)
C. I(2;0;0)
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. 6x + 4y + 3z + 12 = 0
B. 6x + 4y + 3z = 0
C. 6x + 4y + 3z - 12 = 0
D. 6x + 4y + 3z - 24 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. M(-1;0;4)
B. M(0;1;2)
C. M(3;4;2)
D. M(4;1;2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. 2x -y +2z -2 = 0 và x - 2y + z -21 = 0
B. x- 2y+ 2z + 3 = 0 và x - 2y + z -21 = 0
C. 2x -y +2z + 3 = 0 và 2x - y + 2z -21 = 0
D. 2x -y +2z + 5 = 0 và x - 2y + 2z -2 = 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A. K(0;0;1)
B. J(0;1;0)
C. I(1;0;0)
D. O(0;0;0)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. x+3y+10=0
B. -4x+12z-10=0
C. x-3y+10=0
D. x-3z+10=0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. H(2;2;3)
B. H(0;-2;1)
C. H(1;0;2)
D. H(-1;-4;0)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.